Gọi A'(a,b) và B'(c,d) lần lượt là ảnh của A và B qua phép đối xứng trục qua trục Ox
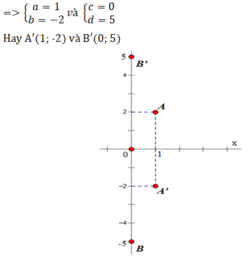
Gọi A'(a,b) và B'(c,d) lần lượt là ảnh của A và B qua phép đối xứng trục qua trục Ox

Tìm ảnh của các điểm A(1;2), B(5;0) qua phép đối xứng trục Oy.
Trong mặt phẳng tọa độ Oxy cho điểm A(-1;2) và đường thẳng d có phương trình 3 x + y + 1 = 0 . Tìm ảnh của A và d.
a. Qua phép tịnh tiến theo vectơ v=(2;1);
b. Qua phép đối xứng trục Oy;
c. Qua phép đối xứng qua gốc tọa độ;
d. Qua phép quay tâm O góc 90 o .
Cho A(2;–1). Ảnh của A qua phép đối xứng trục qua Oy là A’, ảnh của A’ qua phép đối xứng trục qua Ox là A”có toạ độ là:
A. (–2;–1)
B. (2;1)
C. (1;–2)
D. (–2;1)
Trong mặt phẳng tọa độ Oxy, cho biết A(3,5) Tìm tọa độ A’ là ảnh của điểm A qua phép đối xứng trục Ox.
A. A'(-3;-5)
B. A'(5;3)
C. A'(-3;5)
D. A'(3;-5)
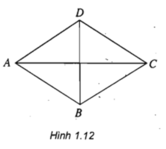
Cho hình thoi ABCD (h.1.12). Tìm ảnh của các điểm A, B, C, D qua phép đối xứng trục AC.
Cho A(8;2). Ảnh của A qua phép đối xứng trục qua Ox có toạ độ là:
A. (8;2)
B. (2;8)
C. (8;–2)
D. (2;–8)
Trong mặt phẳng tọa độ Oxy, cho điểm M(3; -5), đường thẳng d có phương trình 3x + 2y – 6 = 0 và đường tròn (C) có phương trình x 2 + y 2 − 2 x + 4 y – 4 = 0 . Tìm ảnh của M, d, và (C) qua phép đối xứng qua trục Ox
Trong mặt phẳng Oxy cho A(1;-2) và B(3;1). Tìm ảnh của A, B và đường thẳng AB qua phép đối xứng trục Ox.
Trong mặt phẳng Oxy, cho v → = ( 2 ; 0 ) và điểm M(1; 1).
a) Tìm tọa độ của điểm M’ là ảnh của điểm M qua phép dời hình có được bằng cách thực hiện liên tiếp phép đối xứng qua trục Oy và phép tịnh tiến theo vectơ v →
b) Tìm tọa độ của điểm M" là ảnh của điểm M qua phép dời hình có được bằng cách thực hiện liên tiếp phép tịnh tiến theo vectơ v → và phép đối xứng qua trục Oy.