- Ta có:
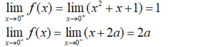
- Suy ra hàm số liên tục tại x = 0 khi và chỉ khi:
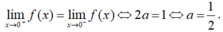
Chọn A.
- Ta có:
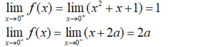
- Suy ra hàm số liên tục tại x = 0 khi và chỉ khi:
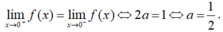
Chọn A.
Tìm a để các hàm số f ( x ) = 4 x + 1 - 1 a x 2 + ( 2 a + 1 ) x k h i x ≠ 0 3 k h i x = 0 liên tục tại x = 0.
A. 1 2
B. 1 4
C. - 1 6
D. 1
Cho hàm số f ( x ) = sin 5 x 5 x x ≠ 0 a + 2 x = 0 . Tìm a để f(x) liên tục tại x = 0.
A. 1.
B. -1.
C. -2.
D. 2.
Giá trị của k để hàm só f(x)=\(\hept{\begin{cases}\frac{x^{2019}+x-2}{\sqrt{2020+1}-\sqrt{x+2020}}\\2k\end{cases}}\) liên tục tại x0=1 có dạng \(k=\frac{a\sqrt{b}}{c}\), với a,b,c là các số nguyên và \(\frac{a\sqrt{b}}{c}\)
là phân số tới giản. tính a-b+c ( f(x) = 2k , khi x<=1; f(x)=... khi x>1)
2. Gía trị của a để các hàm số \(f\left(x\right)=\left\{{}\begin{matrix}x+2a\left(khix< 0\right)\\x^2+x+1\left(khix\ge0\right)\end{matrix}\right.\)liên tục tại x=0
3. Chứng minh phương trình \(x^4-x-2=0\) luôn có nghiệm thuộc khoảng (1;2)
Câu 1:
Cho f(x)= \(\dfrac{\sqrt{x+2}-\sqrt{2-x}}{x}\), x≠0. Phải bổ sung thêm giá trị f(0) bằng bao nhiêu thì hàm số f(x) liên tục tại x=0?
Câu 2:
Xét tính liên tục của hàm số
a, f(x)= \(\left\{{}\begin{matrix}x+\dfrac{3}{2}\\\dfrac{\sqrt{x+1}-1}{\sqrt[3]{1+x}-1}\end{matrix}\right.\)khi x≤0 và x>0 tại xo=0
b, f(x)= \(\left\{{}\begin{matrix}\dfrac{x^3-x^2+2x-2}{x-1}\\3x+a\end{matrix}\right.\)với x<1 và với x≥1, xo=1
Chọn giá trị f(0) để các hàm số f ( x ) = 2 x + 1 - 1 x ( x + 1 ) liên tục tại điểm x = 0.
A. 1
B. 2
C. 3
D. 4
Chọn giá trị f(0) để các hàm số f ( x ) = 2 x + 1 - 1 x ( x + 1 ) liên tục tại điểm x= 0.
A. 1
B. 2
C. 3
D. 4
Chọn giá trị f(0) để các hàm số f ( x ) = x + 1 + x - 1 3 x k h i x ≢ 0 2 k h i x = 0 liên tục tại điểm x= 0.
A. Hàm số liên tục tại x 0 = 0
B. Hàm số liên tục tại mọi điểm nhưg gián đoạn tại x 0 = 0
C. Hàm số không liên tục tại x 0 = 0
D. Tất cả đều sai
Cho hàm số f ( x ) = x 2 sin 1 x n ế u x ≠ 0 A n ế u x = 0
Xác định A để f(x) liên tục tại x = 0. Với giá trị A tìm được, hàm số có đạo hàm tại x = 0 không?