ĐKXĐ.: x ≥ 0
TXĐ: D = 0 ; + ∞
Chọn đáp án C.
ĐKXĐ.: x ≥ 0
TXĐ: D = 0 ; + ∞
Chọn đáp án C.
Xác định một hàm số y = f(x) thoả mãn đồng thời các điều kiện sau
f(x) xác định trên R
y = f(x) liên tục trên (−∞;0) và trên [0;+∞) nhưng gián đoạn tại x = 0
Tập xác định của hàm số y=cotx/cosx-1 A . R\{kpi/2 , k thuộc z} B . R\{pi/2+kpi,k thuộc z} C . R\{kpi,k thuộc z} D . R
Tìm tập xác định D của hàm số y = 1 - sin x 1 + sin x
![]()
![]()
![]()
![]()
Cho hàm số f(x) xác định trên R bởi f ( x ) = x 2 . Giá trị f ' (0) bằng
A. 0
B. 2
C. 1
D. không tồn tại
Xác định a ; b để các hàm số f ( x ) = sin x k h i x ≤ π 2 a x + b k h i x > π 2 liên tục trên R
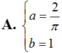
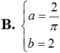
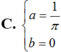
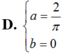
Trong các hàm số sau, có bao nhiêu hàm số là hàm chẵn trên tập xác định của nó?
y = cot 2x; y = cos(x + π); y = 1 – sin x; y = tan2016x
A. 1.
B. 2
C. 3
D. 4
cho hàm số y=f=(x)sinx phieu nào sau đây ddungs?
a. txđ D=R{0}
b. đồ thị có tâm đối xứng
c.đồ thị có trục đối xứng
d.có tập giá trị là [-1,1]
Cho hàm số \(y=-x^2+3x-2\) có đồ thị (D) a;Tính đạo hàm của hàm số tại điểm y',\(x_0\) thuộc R b,Viết phương trình tiếp tuyến của (P) tại điểm có hoành độ \(x_0=2\) c,Viết phương trình tiếp tuyến của (P) tại điểm có tung độ \(y_0=0\); d, Viết phương trình tiếp tuyến của (P) biết tiếp tiếp vuông góc với đường thẳng y'=x+3
1. tập xác định của hàm số \(y=\sqrt{sin8x+5}\)
A. D=R
B. D=R\\(\left\{-k2\pi,k\varepsilon Z\right\}\)
C. D=R\\(\left\{-\dfrac{\pi}{2}+k2\pi,k\varepsilon Z\right\}\)
D. D=R\\(\left\{-\pi+k2\pi,k\varepsilon Z\right\}\)
2. giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số \(y=\sqrt{sin3x}\)
A. M=1;m=-3
B. M=3;m=1
C. M=1;m=-1
D. M=1;m=0
\(\left\{-k2\pi,k\varepsilon Z\right\}\)\(\left\{-k2\pi,k\varepsilon Z\right\}\)
Cho hàm số y=f(x) xác định trên R và lim x → ∞ f ( x ) = a , lim x → x 0 f ( x ) = b . Tiệm cận ngang của đồ thị hàm số đã cho là đường thẳng
A.x=b
B.y=b
C.x=a
D.y=a