Đáp án A
Phương pháp:
Hàm số y = lnx xác định ⇔ x > 0
Cách giải:
Điều kiện xác định: -x2 + 5x - 6 > 0 ⇔ 2 < x < 3
Vậy tập xác định của hàm số y = ln(-x2 + 5x - 6) là (2;3)
Đáp án A
Phương pháp:
Hàm số y = lnx xác định ⇔ x > 0
Cách giải:
Điều kiện xác định: -x2 + 5x - 6 > 0 ⇔ 2 < x < 3
Vậy tập xác định của hàm số y = ln(-x2 + 5x - 6) là (2;3)
Tìm tập hợp nghiệm của phương trình 2 x 2 - x - 4 = 0
A. {1;2} B. {2;3}
C. {-2;3} D. {2;-3}
Tìm tập hợp nghiệm của phương trình 2 x 2 - x - 4 = 0
A. {1;2} B. {2;3}
C. {-2;3} D. {2;-3}
Tìm giá trị lớn nhất của hàm số f(x)=x(2-ln x) trên đoạn [2;3].
A.![]()
B. ![]()
C. ![]()
D. ![]()
Cho hàm số y = f(x) = 2 x + m x - 1 . Tính tổng các giá trị của tham số m để m a x [ 2 ; 3 ] f ( x ) - m i n [ 2 ; 3 ] f ( x ) = 2.
A. -4
B. -2
C. -1
D. -3
Cho hàm số y = f(x) = 2 x + m x - 1 . Tính tổng các giá trị của tham số m để m a x [ 2 ; 3 ] f ( x ) - m i n [ 2 ; 3 ] f ( x ) = 2
A. -4
B. -2
C. -1
D. -3
Cho hàm số y = f(x) xác định, liên tục trên đoạn [-2;3] và có đồ thị là đường cong trong hình vẽ bên. Tìm số điểm cực đại của hàm số y = f(x) trên đoạn [-2; 3]
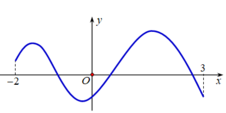
A. 1
B. 0
C. 2.
D. 3
Cho hàm số y=f(x), x ∈ - 2 ; 3 có đồ thị như hình vẽ. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số f(x) trên đoạn - 2 ; 3 . Giá trị của M+n là
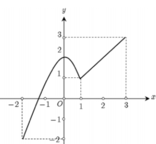
A. 6
B. 1
C. 5
D. 3
Cho hàm số y=f(x), x ∈ - 2 ; 3 có đồ thị như hình vẽ. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số f(x) trên đoạn - 2 ; 3 . Giá trị của S=M+m là:
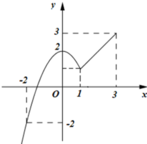
A. 6
B. 3
C. 5
D. 1
Cho hàm số y = f x , x ∈ - 2 ; 3 có đồ thị như hình vẽ. Gọi M, m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn - 2 ; 3 . Giá trị của biểu thức 2 m + log 9 M bằng?
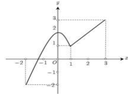
A. 1 8
B. 3 8
C. 3 4
D. 3 2
Giá trị lớn nhất của hàm số y = x ( 2 - ln x ) trên đoạn [2;3] bằng
A.3
![]()
![]()
D.e