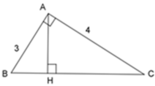
Áp dụng định lý Pytago vào tam giác vuông ABC ta có:
A B 2 + A C 2 = B C 2 ⇔ 3 2 + 4 2 = B C 2
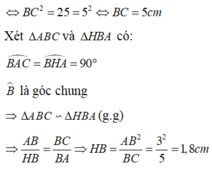


Áp dụng định lý Pytago vào tam giác vuông ABC ta có:
A B 2 + A C 2 = B C 2 ⇔ 3 2 + 4 2 = B C 2
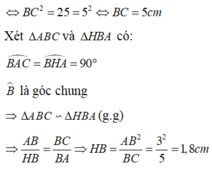

Cho tam giác ABC vuông tại A, AB<AC, có AH là đường cao(H thuộc BC). Chứng minh rằng:
a) Tam giác HBA đồng dạng tam giác ABC và HB*AC= HA*AB
b) HA^2=hb*HC
c) Gọi M là trung điểm AH. Trên tia đối tia AC lấy N sao cho AN=1/2AC. Chứng minh: tam giác BHM đồng dạng tam giác BAN
d) Góc BMN=90 độ
cho tam giác ABC vuông tại A, AH là đường cao
AB=15cm, AC=20cm, BC=25cm
a. chứng minh tam giác ABC đồng dạng với tam giác HBA
b. chứng minh HA^2=HB.HC
c tính HA. HB , HC
d. kẻ phân giác AD. Tính AD
cho tam giác ABC vuông tại a, có AB=3cm, AC= 4cm. Vẽ đường cao AH ( H thuộc BC)
a) Tính độ dài BC
b) Chứng minh tam giác HBA đồng dạng với tam giác HAC
c) Chứng minh: Ha2 = Hb x HC
d) Kẻ tia phân giác AD( D thuộc BC) tính BD, CD ?
Cho tam giác ABC có dộ dài ba cạnh là BC,AC,AB lần lượt là a,b,c.
Các đường cao tương ứng là ha,hb,hc. tam giác đó là tam giác gì khi biểu thức \(\frac{\left(a+b+c\right)^2}{ha^2+hb^2+hc^2}\)đạt gtnn
Cho tam giác ABC với BC = a, CA = b, AB = c và ba đường cao ứng với ba cạnh lần lượt có độ dài ha,hb,hc Gọi r là khoảng cách từ giao điểm của ba đường phân giác của tam giác đến một cạnh của tam giác. Chứng minh 1/ha+1/hb+1/hc=1/r
cho tam giác vuông ABC vuông tại A đường cao AH
a, cm rằng '' HA2 = HB . HC
nếu biết HB = 1,8 cm và HC = 3,2 cm . tính diện tích tam giác ABC
b. tia pg góc B cắt AC , AH lần lượt ở E và D . chứng minh rằng '' DA/DH × EA/EC =1
cho a, b,c là độ dài ba cạnh của một tam giác. CMR (a^2+b^2+c^^2)(ha^2+hb^2+hc^2) >=36 với ha, hb, hc là 3 đường cao tương ứng
Cho M là điểm nằm trong tam giác ABC, từ M kẻ MA' vuông góc BC, kẻ MB' vuông góc AC, kẻ MC' vuông góc AB( A' thuộc BC, B' thuộc AC, C' thuộc AB). Chứng minh rằng MA'/ha + MB'/hb + MC'/hc = 1
(ha, hb, hc là đường cao của tam giác hạ lần lượt từ A,B,C xuống các cạnh của tam giác ABC)
Tính diện tích tam giác ABC biết độ dài các đường cao là ha, hb,hc