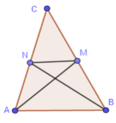
Ta có ABMN là tứ giác có hai đường chéo AM và BN vuông góc
nên có diện tích là: SABMN = 1 2 AB.MN
Hai tam giác AMC và ABC có chung đường cao hạ từ A
nên S A M C S A B C = M C B C = 1 2
=> SAMC = 1 2 SABC (1)
Hai tam giác AMN và AMC có chung đường cao hạ từ M
nên S A M N S A M C = A N A C = 1 2
=> SAMB = 1 2 SABC (2)
Từ (1) và (2) suy ra SAMN = 1 4 SABC
Hai tam giác AMB và ABC có chung đường cao hạ từ A
nên S A M B S A B C = B M B C = 1 2
=> SAMB = 1 2 SABC
Ta có: SABMN = SAMN + SABM
= 1 4 SABC + 1 2 SABC = 3 4 SABC
=> SABC = 4 3 SABMN = 4 3 .AM. 1 2 BN = 2 3 AM.BN
Đáp án cần chọn là: D

