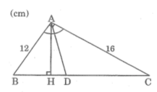
Ta có: S A B C = 1/2.AB.AC = 1/2.AH.BC
Suy ra: AB.AC = AH.BC
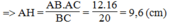
Trong tam giác vuông AHB, ta có: ∠ A H B = 90 0
Theo định lí Pi-ta-go, ta có: A B 2 = A H 2 + H B 2
Suy ra: H B 2 = A B 2 - A H 2 = 12 2 - 9 , 6 2 = 51,84 ⇒ HB =7,2 (cm)
Vậy HD = BD – HB = 60/7 - 7,2 ≈ 1,37 (cm)
Trong tam giác vuông AHD, ta có: ∠ A H D = 90 0
Theo định lí Pi-ta-go, ta có:
A D 2 = A H 2 + H D 2 = 9 , 6 2 + 1 , 37 2 = 94,0369
Suy ra: AD ≈ 9,70 (cm)