Question

Tam giác ABC có đường trung tuyến AM bằng nửa cạnh BC. Chứng minh rằng ∠(BAC) = 90o

Answer 1

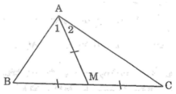
Vì AM là đường trung tuyến của ΔABC nên BM = MC = 1/2 BC

Mà AM = 1/2 BC (gt) nên: AM = BM = MC.

Tam giác AMB có AM = MB nên ΔAMB cân tại M

Suy ra: ∠B = ∠A1 (tính chất tam giác cân) (1)

Tam giác AMC có AM = MC nên ΔAMC cân tại M

Suy ra: ∠C = ∠A2 (tính chất tam giác cân) (2)

Từ (1) và (2) suy ra: ∠B + ∠C = ∠A1 + ∠A2 = ∠(BAC) (3)

Trong ΔABC ta có:

∠B + ∠C + ∠(BAC) = 180o (tổng ba góc trong tam giác) (4)

Từ (3) và (4) suy ra: ∠(BAC) + ∠(BAC) = 180o ⇔ 2∠(BAC) = 180o

Hay ∠(BAC) = 90o.

Vậy ΔABC vuông tại A.