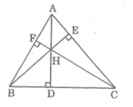
Xét △ AFH và △ CDH, ta có:
∠ (AFH) = ∠ (CDH) = 90 0
∠ (AHF) = ∠ (CHD) (đối đỉnh)
Suy ra: △ AFH đồng dạng △ CDH (g.g)
Suy ra: 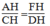
Suy ra: AH.DH = CH.FH (1)
Xét △ AEH và △ BDH,ta có:
∠ (AEH) = ∠ (BDH) = 90 0
∠ (AHE) = ∠ (BHD) (đối đỉnh)
Suy ra: △ AEH đồng dạng △ BDH (g.g)
Suy ra: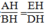
Suy ra: AH.DH = BH.EH (2)
Từ (1) và (2) suy ra: AH.DH = BH.EH = CH.FH.