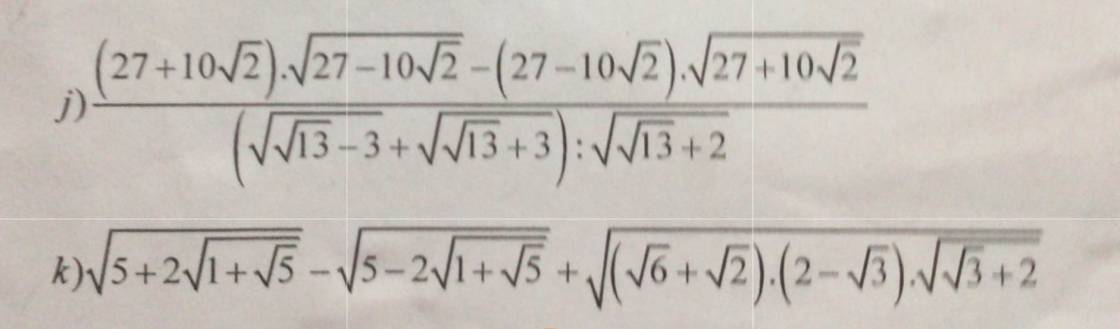k) Đặt \(A=\sqrt{5+2\sqrt{1+\sqrt{5}}}-\sqrt{5-2\sqrt{1+\sqrt{5}}}+\sqrt{\left(\sqrt{6}+\sqrt{2}\right).\left(2-\sqrt{3}\right).\sqrt{\sqrt{3}+2}}\)Đặt \(B=\sqrt{5+2\sqrt{1+\sqrt{5}}}-\sqrt{5-2\sqrt{1+\sqrt{5}}}>0\)
\(\Rightarrow B^2=5+2\sqrt{1+\sqrt{5}}-2\sqrt{\left(5+2\sqrt{1+\sqrt{5}}\right)\left(5-2\sqrt{1+\sqrt{5}}\right)}+5-2\sqrt{1+\sqrt{5}}\)
\(=10-2\sqrt{25-4\left(1+\sqrt{5}\right)}\)
\(=10-2\sqrt{21-4\sqrt{5}}\)
\(=10-2\sqrt{\left(2\sqrt{5}-1\right)^2}\)
\(=10-2\left|2\sqrt{5}-1\right|\)
\(=10-4\sqrt{5}+2=12-4\sqrt{5}\)
\(\Rightarrow B=\sqrt{12-4\sqrt{5}}=\sqrt{2}.\sqrt{6-2\sqrt{5}}=\sqrt{2}.\sqrt{\left(\sqrt{5}-1\right)^2}=\sqrt{2}.\left|\sqrt{5}-1\right|=\sqrt{10}-\sqrt{2}\)
Đặt \(C=\sqrt{\left(\sqrt{6}+\sqrt{2}\right).\left(2-\sqrt{3}\right).\sqrt{\sqrt{3}+2}}\)
\(=\sqrt{\sqrt{2}.\left(\sqrt{3}+1\right).\left(2-\sqrt{3}\right).\sqrt{\sqrt{3}+2}}\)
\(=\sqrt{\left(\sqrt{3}+1\right).\left(2-\sqrt{3}\right).\sqrt{2\sqrt{3}+4}}\)
\(=\sqrt{\left(\sqrt{3}+1\right).\left(2-\sqrt{3}\right).\sqrt{\left(\sqrt{3}+1\right)^2}}\)
\(=\sqrt{\left(\sqrt{3}+1\right).\left(2-\sqrt{3}\right).\left|\sqrt{3}+1\right|}\)
\(=\sqrt{\left(\sqrt{3}+1\right)^2}.\sqrt{2-\sqrt{3}}\)
\(=\left(\sqrt{3}+1\right).\sqrt{2-\sqrt{3}}\)
\(=\dfrac{\left(\sqrt{3}+1\right).\sqrt{4-2\sqrt{3}}}{\sqrt{2}}\)
\(=\dfrac{\left(\sqrt{3}+1\right).\left|\sqrt{3}-1\right|}{\sqrt{2}}\)
\(=\dfrac{3-1}{\sqrt{2}}=\sqrt{2}\)
\(\Rightarrow A=B+C=\sqrt{10}-\sqrt{2}+\sqrt{2}=\sqrt{10}\)
- Vậy...