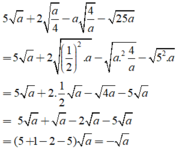Các câu hỏi tương tự
Bài 1: Cho biểu thức P = √x √x x-4 √x−2+√x+2) 2√x (với x > 0 và x ≠ 4) a) Rút gọn biểu thức P b) Tìm x để P = 3 Cho biểu thức P = √x √x x-25 + √x-5 √x+5) 2√x (với x > 0 và x ≠ 25) a) Rút gọn biểu thức P b) Tìm x để P = 2
Rút gọn biểu thức M=\(\sqrt{a^4}\)-\(a\sqrt{a^2}\)-\(\dfrac{b}{2}\sqrt{4b^2}\)-b2 (a≤0; b≥0) ta được:
A.2b2 B.2a2 C.0 D.2(a2-b2)
rút gọn các biểu thức sau
c,\(\sqrt{4+2\sqrt{3}}+\sqrt{4-2\sqrt{3}}\) d,\(5\sqrt{16a}-4\sqrt{25a}-2\sqrt{100a}+\sqrt{169a}\) với a ≥ 0
e,\(5\sqrt{4a}-4\sqrt{a^2}-\sqrt{100a}\) với a ≥ 0 f,\(3\sqrt{4a^6}-5^3\) với a ≤ 0
Rút gọn các biểu thức:
a) √0,49a^2 với a<0
b)√25(7-a)^2 với a>=7
c)√a^4(a-2)^2 với a>0
Rút gọn biểu thức:
D
2
(
a
+
b
)
b
b
a
2
+
2
ab...
Đọc tiếp
Rút gọn biểu thức: D = 2 ( a + b ) b b a 2 + 2 ab + b 2 với a, b > 0, ta được:
A. 29
B. 2
C. 10
D. 25
Rút gọn các biểu thức sau:
a) $\sqrt{9a^4}$
b) 2$\sqrt{a^{2}}$- 5a (với a<0)
c) $\sqrt{16(1+4x+4x^2)}$ với x $\geq$ $\frac{1}{2}$
d) $\frac{1}{a-3}$$\sqrt{9(a^2-3a+9)}$ với a<3
Rút gọn biểu thức
E
a
-
b
2
a
ab
(
a
-
b
)...
Đọc tiếp
Rút gọn biểu thức E = a - b 2 a ab ( a - b ) 2 với 0 < a < b, ta được:
A. b 2
B. a b 2
C. − b 2
D. b 2 a
Cho A = (x + 3√x)/(x - 25) + 1/(√x + 5) và B = (√x + 2)/(√x - 5) với x > = 0, x # 25
a) Rút gọn biểu thức A. Tìm x để P = A/B = 4/7
b) Tìm các giá trị x nguyên để P nhận giá trị nguyên
Bài 2. Cho biểu thức : P = \(\dfrac{a+4\sqrt{a}+4}{\sqrt{a}+2}\)+\(\dfrac{4-a}{2-\sqrt{a}}\)( Với a ![]() 0 ; a ≠ 4 )
0 ; a ≠ 4 )
a) Rút gọn biểu thức P; b)Tìm giá trị của a sao cho P = a + 1.
1. Cho bt P= (1/√x+2 + 1/√x-2 ) . √x-2/√x với x>0, x khác 4
a) rút gọn P
b) tìm x để P>1/3
c) tìm các giá trị thực của x để Q=9/2P có giá trị nguyên
2. Cho 2 biểu thức
A= 1-√x / 1+√ x và B= ( 15-√x/ x-25 + 2/√x+5) : √x+1/√ x-5 với x lớn hơn hoặc bằng 0, x khác 25
a) tính giá trị của A khi x= 6-2√5
b) rút gọn B
c) tìm a để pt A-B=a có nghiệm