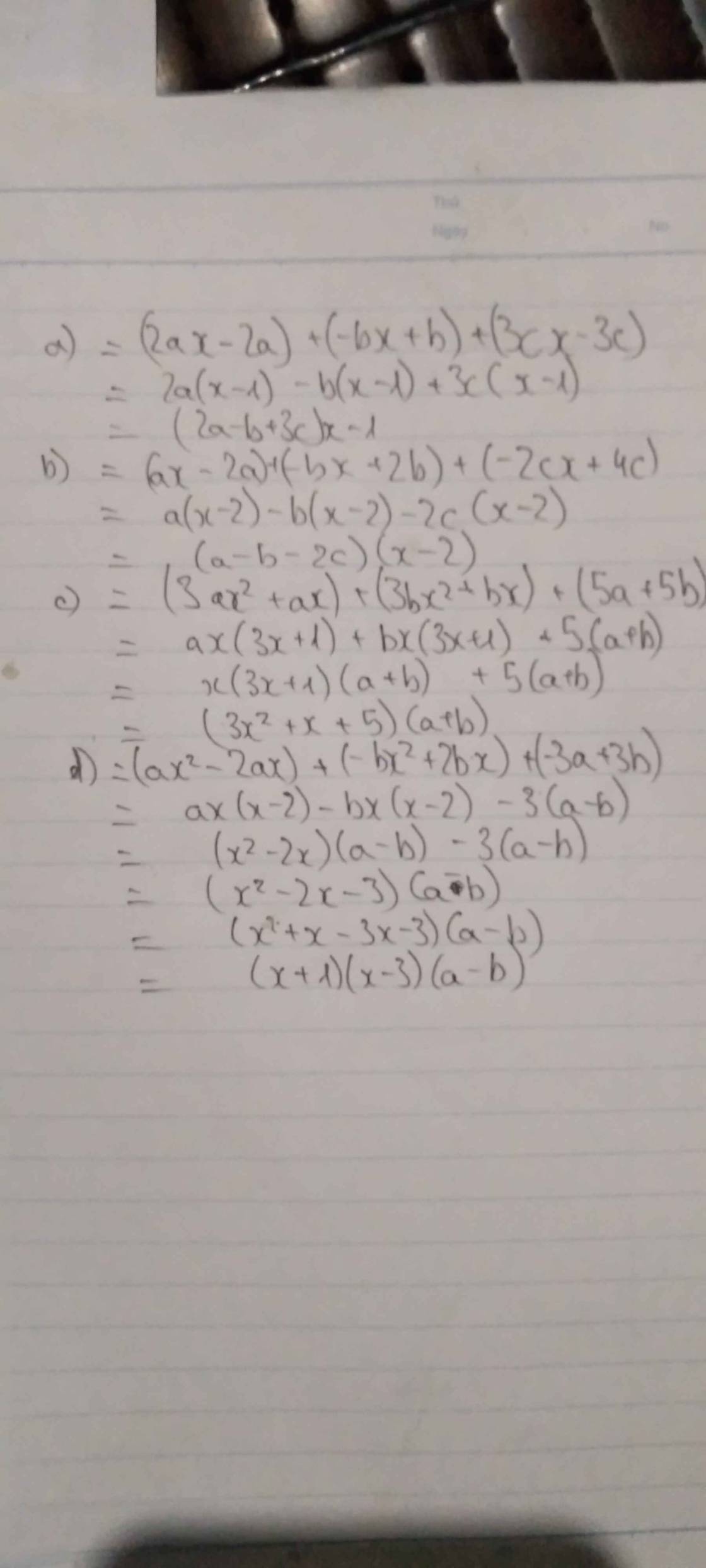Question

Phân tích thành nhân tử (mọi người làm chi tiết ạ)

\(2ax-bx+3cx-2a+b-3c\)

\(ax-bx-2cx-2a+2b+4c\)

\(3ax^2 +3bx^2 +ax+bx+5a+5b\)

\(ax^2 -bx^2 -2ax+2bx-3a+3b\)

Answer 1

  

Answer 2

\(2ax-bx+3cx-2a+b-3c\\ =x\left(2a-b+3c\right)-\left(2a-b+3c\right)\\ =\left(x-1\right)\left(2a-b+3c\right)\)

 

\(ax-bx-2cx-2a+2b+4c\\ =x\left(a-b-2c\right)-2\left(a-b-2c\right)\\ =\left(x-2\right)\left(a-b-2c\right)\)

 

\(3ax^2+3bx^2+ax+bx+5a+5b\\ =3x^2\left(a+b\right)+x\left(a+b\right)+5\left(a+b\right)\\ =\left(3x^2+x+5\right)\left(a+b\right)\)

 

\(ax^2-bx^2-2ax+2bx-3a+3b\\ =x^2\left(a-b\right)-2x\left(a-b\right)-3\left(a+b\right)\\ =\left(x^2-2x-3\right)\left(a+b\right)\\ =\left(x+1\right)\left(x-3\right)\left(a+b\right)\)