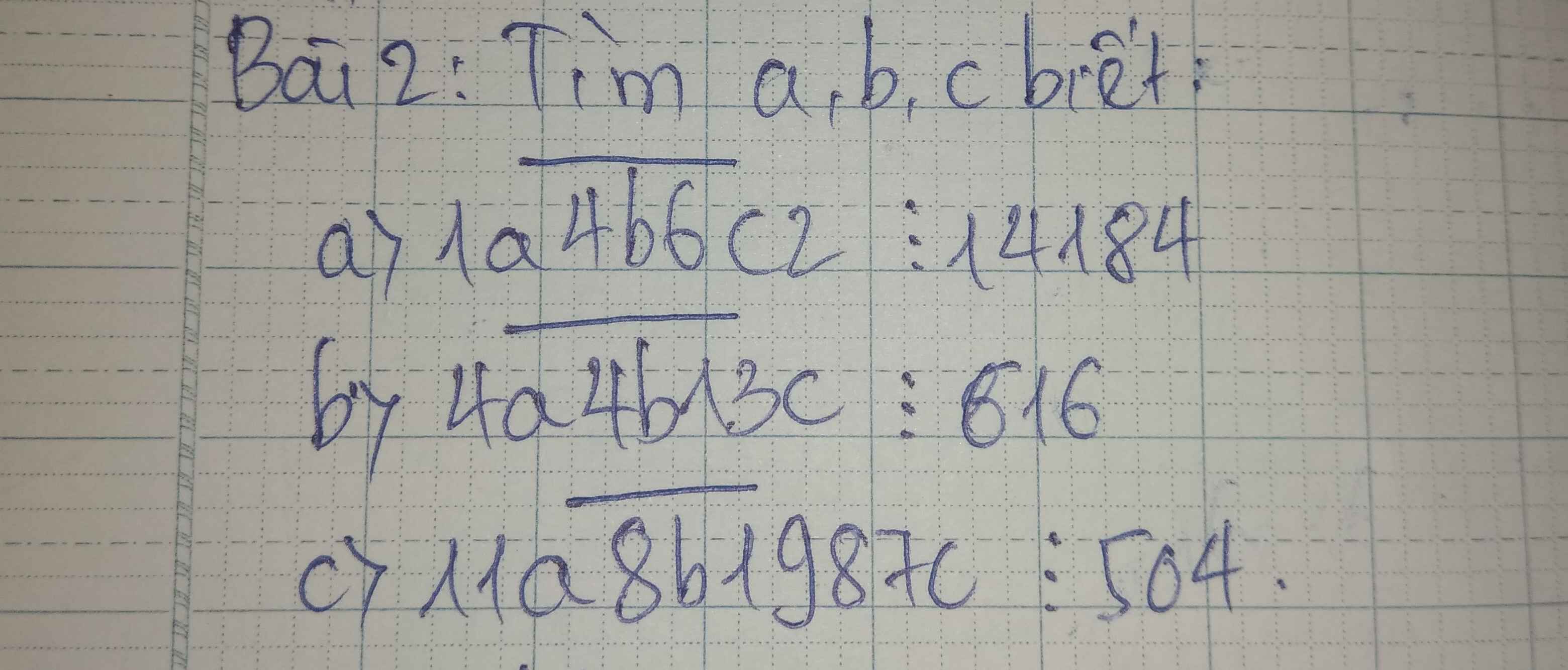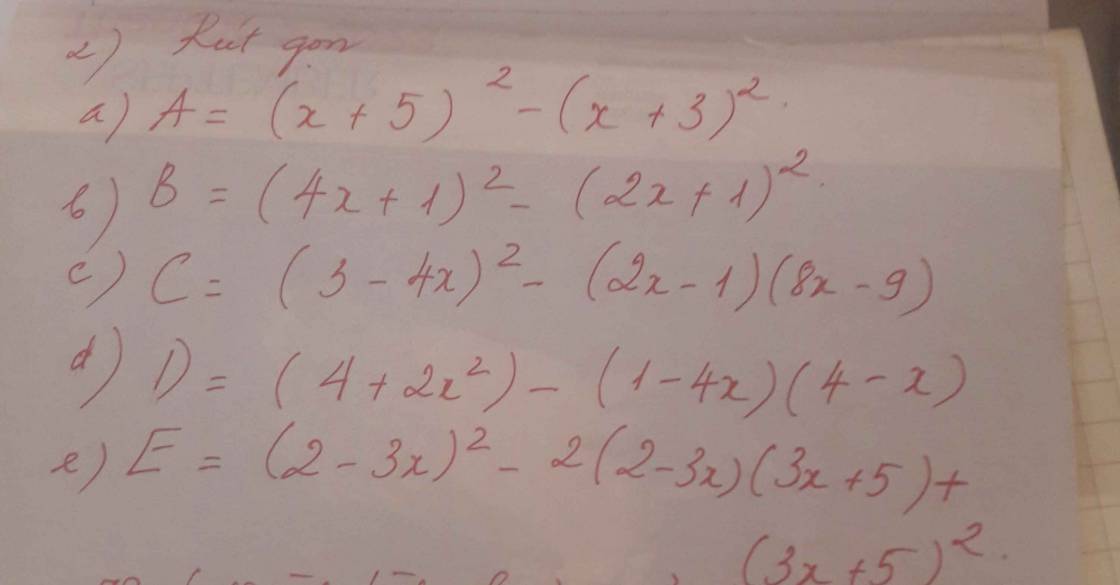1. a
$(3x+5)^2=(3x)^2+2.3x.5+5^2$
$=9x^2+30x+25$
1.b
$(6x^2+\frac{1}{3})^2=(6x^2)^2+2.6x^2.\frac{1}{3}+(\frac{1}{3})^2$
$=36x^4+4x^2+\frac{1}{9}$
1.c
$(5x-4y)^2=(5x)^2-2.5x.4y+(4y)^2$
$=25x^2-40xy+16y^2$
1.d
(2x^2y-3y^3x)^2=(2x^2y)^2-2.2x^2y.3y^3x+(3y^3x)^2$
$=4x^4y^2-12x^3y^4+9x^2y^6$
1.e
$(5x-3)(5x+3)=(5x)^2-3^2=25x^2-9$
1.f
$(6x+5y)(6x-5y)=(6x)^2-(5y)^2=36x^2-25y^2$
1.g
$(-4xy-5)(5-4xy)=(-4xy-5)(-4xy+5)$
$=(-4xy)^2-5^2=16x^2y^2-25$
1.h
$(a^2b+ab^2)(ab^2-a^2b)=(ab^2+a^2b)(ab^2-a^2b)$
$=(ab^2)^2-(a^2b)^2=a^2b^4-a^4b^2$
1.i
$(3x-4)^2+2(3x-4)(4-x)+(4-x)^2$
$=[(3x-4)+(4-x)]^2=(2x)^2=4x^2$
1.j
$(3a-1)^2+2(9a^2-1)+(3a+1)^2$
$=(3a-1)^2+2(3a-1)(3a+1)+(3a+1)^2$
$=[(3a-1)+(3a+1)]^2=(6a)^2=36a^2$
1.k
(a^2+ab+b^2)(a^2-ab+b^2)-(a^4+b^4)$
$=(a^2+b^2)^2-(ab)^2-(a^4+b^4)$
$=a^4+b^4+2a^2b^2-a^2b^2-a^4-b^4$
$=a^2b^2$
Bài 2:
a. $x^2+2x+1=x^2+2.x.1+1^2=(x+1)^2$
b. $1-4x+4x^2=1^2-2.1.2x+(2x)^2=(1-2x)^2$
c. $4x^4-4x^2+1=(2x^2)^2-2.2x^2.1+1^2=(2x^2-1)^2$
d. $36a^2-60ab+25b^2=(6a)^2-2.6a.5b+(5b)^2$
$=(6a-5b)^2$
e. $a^2+9-6a=a^2-2.a.3+3^2=(a-3)^2$
f. $9x^4+16y^6-24x^2y^3=(3x^2)^2-2.3x^2.4y^3+(4y^3)^2$
$=(3x^2-4y^3)^2$
Bài 3.
$Q=(20^2+18^2+16^2+...+4^2+2^2)-(19^2+17^2+....+3^2+1^2)$
$=(20^2-19^2)+(18^2-17^2)+(16^2-15^2)+....+(2^2-1^2)$
$=(20-19)(20+19)+(18-17)(18+17)+(16-15)(16+15)+...+(2-1)(2+1)$
$=20+19+18+17+...+2+1$
$=\frac{20(20+1)}{2}=210$
Bài 4.
a.
$A=x^2-2x+5=(x^2-2x+1)+4$
$=(x-1)^2+4$.
Vì $(x-1)^2\geq 0$ với mọi $x\in\mathbb{R}$ nên $A=(x-1)^2+4\geq 4$
Vậy $A_{\min}=4$. Giá trị này đạt tại $(x-1)^2=0\Leftrightarrow x=1$
b.
$B=x^2-x+1=x^2-2.x.\frac{1}{2}+(\frac{1}{2})^2+\frac{3}{4}$
$=(x-\frac{1}{2})^2+\frac{3}{4}$
Vì $(x-\frac{1}{2})^2\geq 0$ với mọi $x\in\mathbb{R}$ nên $B\geq \frac{3}{4}$
Vậy $B_{\min}=\frac{3}{4}$. Giá trị này đạt tại $(x-\frac{1}{2})^2=0\Leftrightarrow x=\frac{1}{2}$
Bài 5.
a.
$C=(x-1)(x+2)(x+3)(x+6)$
$=(x-1)(x+6)(x+2)(x+3)=(x^2+5x-6)(x^2+5x+6)$
$=(x^2+5x)^2-6^2=(x^2+5x)^2-36$
Vì $(x^2+5x)^2\geq 0, \forall x\in\mathbb{R}$ nên $C\geq -36$
Vậy $C_{\min}=-36$. Giá trị này đạt tại $x^2+5x=0\Leftrightarrow x=0$ hoặc $x=-5$
b)
$D=x^2+5y^2-2xy+4y+3$
$=(x^2-2xy+y^2)+(4y^2+4y+1)+2$
$=(x-y)^2+(2y+1)^2+2$
$\geq 0+0+2=2$
Vậy $D_{\min}=2$
Giá trị này đạt tại \(\left\{\begin{matrix} x-y=0\\ 2y+1=0\end{matrix}\right.\Leftrightarrow x=y=\frac{-1}{2}\)
Bài 6:
$A=-x^2-4x-2$
$-A=x^2+4x+2=(x^2+4x+4)-2=(x+2)^2-2\geq 0-2=-2$
$\Rightarrow A\leq 2$
Vậy $A_{\max}=2$. Giá trị này đạt tại $(x+2)^2=0\Leftrightarrow x=-2$
b.
$B=-2x^2-3x+5$
$-B=2x^2+3x-5=2(x^2+\frac{3}{2}x)-5$
$=2[x^2+2.\frac{3}{4}.x+(\frac{3}{4})^2]-\frac{49}{8}$
$=2(x+\frac{3}{4})^2-\frac{49}{8}\geq \frac{-49}{8}$
$\Rightarrow B\leq \frac{49}{8}$
Vậy $B_{\max}=\frac{49}{8}$ khi $x=-\frac{3}{4}$
Bài 7.
$C=(2-x)(x+4)=2x+8-x^2-4x=-x^2-2x+8$
$-C=x^2+2x-8=(x^2+2x+1)-9=(x+1)^2-9\geq -9$
$\Rightarrow C\leq 9$
Vậy $C_{\max}=9$. Giá trị này đạt tại $x+1=0\Leftrightarrow x=-1$
b.
$D=-8x^2+4xy-y^2+3$
$-D=8x^2-4xy+y^2-3$
$=(4x^2-4xy+y^2)+4x^2-3$
$=(2x-y)^2+(2x)^2-3$
$\geq 0+0-3=-3$
$\Rightarrow D\leq 3$
Vậy $D_{\max}=3$. Giá trị này đạt tại $(2x-y)^2=(2x)^2=0$
$\Leftrightarrow x=y=0$
Bài 8.
a.
$A=25x^2-20x+7=(5x)^2-2.5x.2+2^2+3$
$=(5x-2)^2+3\geq 0+3>0$ với mọi $x\in\mathbb{R}$
Tức là $A$ luôn dương với mọi $x\in\mathbb{R}$ (đpcm)
b.
$B=9x^2-6xy+2y^2+1$
$=(9x^2-6xy+y^2)+y^2+1=(3x-y)^2+y^2+1\geq 0+0+1>0$ với mọi $x\in\mathbb{R}$
c.
$E=x^2-2x+y^2+4y+6=(x^2-2x+1)+(y^2+4y+4)+1$
$=(x-1)^2+(y+2)^2+1$
$\geq 0+0+1>0$ với mọi $x,y\in\mathbb{R}$
d.
$D=x^2-2x+2=(x^2-2x+1)+1=(x-1)^2+1\geq 1>0$ với mọi $x\in\mathbb{R}$
Ta có đpcm.
Bài 9.
Gọi $a(a+1)(a+2)(a+3)$ với $a\in\mathbb{N}$ là tích 4 số tự nhiên liên tiếp.
Ta có:
$a(a+1)(a+2)(a+3)+1=a(a+3)(a+1)(a+2)+1$
$=(a^2+3a)(a^2+3a+2)+1$
$=(a^2+3a)^2+2(a^2+3a)+1$
$=(a^2+3a+1)^2$ là một số chính phương với mọi $a\in\mathbb{N}$
Ta có đpcm.
Bài 10.
a.
$P=x(x+2)+y(y-2)-2xy=x^2+2x+y^2-2y-2xy$
$=(x^2-2xy+y^2)+(2x-2y)$
$=(x-y)^2+2(x-y)=7^2+2.7=63$
b.
$V=x^2+4y^2-2x+10+4xy-4y$
$=(x^2+4y^2+4xy)-(2x+4y)+10$
$=(x+2y)^2-2(x+2y)+10$
$=(x+2y)^2-2(x+2y)+1+9=(x+2y-1)^2+9$
$=(5-1)^2+9=16+9=25$
c.
$Q=x^3-3xy(x-y)-y^3-x^2+2xy-y^2$
$=(x^3-3x^2y+3xy^2-y^3)-(x^2-2xy+y^2)$
$=(x-y)^3-(x-y)^2=7^3-7^2=294$



 nhờ mng giúp ạ
nhờ mng giúp ạ