Đáp án B
Phương pháp: ∫udv = uv - ∫vdu
Cách giải:
F(x) = ∫f(x).dx = ∫x.cosx.dx = ∫x.dsinx = x.sinx - ∫sinx.dx = x.sinx + cosx + C
Hàm số F(x) = ln|sin x – cos x| là một nguyên hàm của hàm số
A. f ( x ) = sin x + cos x sin x - cos x
B. f ( x ) = sin x - cos x sin x + cos x
C. f ( x ) = 1 sin x + cos x
D. f ( x ) = 1 sin x - cos x
Giá trị lớn nhất của hàm số f(x) = sin x + cos 2x trên [0; π ] là
A. 5 4
B. 1
C. 2
D. 9 8
Biết F(x) là một nguyên hàm của hàm số f x = e - x + sin x thỏa mãn F(0) = 0. Tìm F(x)?
Biết F(x) là một nguyên hàm của hàm số f(x) = sin x và đồ thị hàm số y = F(x) đi qua điểm M(0;1) . Tính F π 2 .
A. F π 2 = 0
B. F π 2 = 1
C. F π 2 = 2
D. F π 2 = - 1
Biết F(x) là một nguyên hàm của hàm số f(x) = sin 2x + cosx. Giá trị F π 2 - F ( 0 ) bằng
A. 2.
B. 1.
C. -1.
D. 4.
Biết F(x) là một nguyên hàm của hàm f(x) = sin 2x và F π 4 = 1 .Tính F π 6
A. F π 6 = 5 4
B. F π 6 = 0
C. F π 6 = 3 4
D. F π 6 = 1 2
Giải pt : \(\dfrac{\cos x\left(1-2\sin x\right)}{2\cos^2x-\sin x-1}\)= \(\sqrt{3}\)
Hàm số f ( x ) = cos x sin 5 x có một nguyên hàm F(x) bằng
A. 1 8 sin 4 x
B. - 1 8 sin 4 x + 1
C. 4 sin 4 x
D. - 1 4 sin 4 x + 2
Cho hàm số y=f(x). Hàm số f'(x) có biến thiên
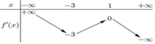
Bất phương trình f(sin x)< -3x + m đúng với mọi x ∈ - π 2 ; π 2 khi và chỉ khi
A. m ≥ f ( 1 ) + 3 π 2
B. m > f ( - 1 ) - 3 π 2
C. m > f ( π 2 ) + 3 π 2
D. m > f ( 1 ) + 3 π 2
Trong các phương trình sau: cos x = 5 - 3 (1); sin x = 1 - 2 (2); sin x + cos x = 2 (3), phương trình nào vô nghiệm?
A. (2)
B. (1)
C. (3)
D. (1) và (2)
