Đáp án là A.
Pt ⇔ 3 x + 1 + 6 2 ≥ 7 − 10 − x ⇔ 3 x + 1 + 2 10 − x ≥ 8
⇔ 4 3 x + 1 10 − x ≥ x + 23 ⇔ x < − 23 − 1 3 ≤ x ≤ 10 x ≥ − 23 49 x 2 − 418 x + 369 ≤ 0 ⇔ x ≥ − 23 1 ≤ x ≤ 369 49 ⇔ 1 ≤ x ≤ 369 49 .
Đáp án là A.
Pt ⇔ 3 x + 1 + 6 2 ≥ 7 − 10 − x ⇔ 3 x + 1 + 2 10 − x ≥ 8
⇔ 4 3 x + 1 10 − x ≥ x + 23 ⇔ x < − 23 − 1 3 ≤ x ≤ 10 x ≥ − 23 49 x 2 − 418 x + 369 ≤ 0 ⇔ x ≥ − 23 1 ≤ x ≤ 369 49 ⇔ 1 ≤ x ≤ 369 49 .
Tìm số nghiệm nguyên của bất phương trình log 5 2 3 x - 2 log 2 ( 4 - x ) - log ( 4 - x ) 2 + 1 > 0
A. 3
B. 1
C. 0
D. 2
Biết rằng tập nghiệm S của bất phương trình log - x 2 + 100 x - 2400 < 2 có dạng S = a ; b \ x ∘ . Giá trị của a + b - x ∘ bằng:
A. 150.
B. 100.
C. 30.
D. 50.
Tìm số nghiệm của phương trình x - 1 2 e x - 1 - log 2 = 0
A. 4
B. 3
C. 2
D. 0
Tích các nghiệm của phương trình log 2 x + 2 - log x = 2 là
A. 10 3 - 5 2
B. 10 3 + 2 2
C. 10 3 + 5 2
D. 10 3 - 2 2
Tìm tất cả các nghiệm của phương trình log x + log ( x - 9 ) = 1
A. {10}
B. {9}
C. {1;9}
D. {-1;10}
Cho x ϵ (0;π/2). Biết log(sinx)+log(cosx)=-1 và log(sinx+cosx)=1/2(logn-1). Giá trị của n là
A. 11.
B. 12.
C. 10.
D. 15.
Cho hàm số y = f (x) liên tục trên R có đồ thị như hình vẽ.
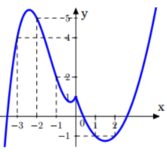
Biết trên ( - ∞ ; - 3 ) ∪ ( 2 ; + ∞ ) t h ì f ' ( x ) > 0 . Số nghiệm nguyên thuộc (-10; 10) của bất phương trình [ f ( x ) + x - 1 ] ( x 2 - x - 6 ) > 0 là
A. 9
B. 10
C. 8
D. 7
Cho a,b,c là các số thực dương thỏa mãn a log 5 2 = 4 , b log 4 6 = 1 , log , c log 7 3 = 49 Tính giá trị của biểu thức T = a log 2 2 5 + b log 4 2 6 + 3 c log 7 2 3
A. T=126
B. T = 5 + 2 3
C. T=88
D. T = 3 - 2 3
Có tất cả bao nhiêu số nguyên m để phương trình log ( m - x ) = 3 log ( 4 - 2 x - 3 ) có hai nghiệm thực phân biệt.
A. 6.
B. 2.
C. 3.
D. 5.