Chọn D
Hàm số y = f x có lim x → - ∞ f x = 2019
thì đồ thị hàm số có 1 đường TCN là y = 2019.
Chọn D
Hàm số y = f x có lim x → - ∞ f x = 2019
thì đồ thị hàm số có 1 đường TCN là y = 2019.
Số tiệm cận ngang của đồ thị hàm số y = | x | - 2018 x + 2019 là
A. 1.
B. 3.
C. 2.
D. 0.
Cho hàm số y = f(x) có đạo hàm trên ℝ , thỏa mãn f(2) = f(-2) =2019. Hàm số y = f'(x) có đồ thị hàm số như hình vẽ. Hỏi hàm số g(x)= f x - 2019 2 (1;2). Ngịch biến trên khoảng nào dưới đây
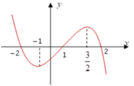
A . 1 ; 2
B . - 2 ; 2
C . 2 ; + ∞
D . - 2 ; - 1
Cho hàm số y = f(x) có đạo hàm trên ℝ , thỏa mãn f(2) = f(-2) = 2019. Hàm số y = f'(x) có đồ thị như hình vẽ. Hỏi hàm số g x = f x - 2019 2 (1;2) nghịch biến trên khoảng nào dưới đây?
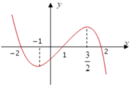
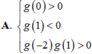
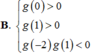
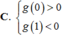
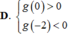
Số đường tiệm cận của đồ thị hàm số y = x + 2019 x - 2019 là
A. 3
B. 1
C. 2
D. 0
Cho hàm số y = f(x) có đạo hàm trên R. Đồ thị hàm số y= f’(x) như hình vẽ bên dưới
Số điểm cực trị của hàm số y= g( x)= f( x- 2017) – 2018x+ 2019 là
A. 1
B. 2
C.3
D. 4
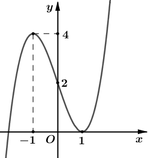
Cho hàm số y = f(x) có đạo hàm liên tục trên ℝ . Đồ thị hàm số y = f'(x) được cho như hình vẽ bên.
Số điểm cực trị của hàm số g(x) = f(x-2017) - 2018x + 2019 là:
A. 1.
B. 3.
C. 2.
D. 0.
Cho các mệnh đề sau
(1) Đường thẳng y = y 0 là đường tiệm cận ngang của đồ thị hàm số y = f(x) nếu lim x → x 0 f x = y 0 h o ặ c lim x → x 0 f x = y 0
(2) Đường thẳng y = y 0 là đường tiệm cận ngang của đồ thị hàm số y = f(x) nếu lim x → - ∞ f x = y 0 h o ặ c lim x → + ∞ f x = y 0
(3) Đường thẳng x = x 0 là đường tiệm cận đứng của đồ thị hàm số y = f(x) nếu lim x → x 0 + f x = + ∞ h o ặ c lim x → x 0 - f x = - ∞
(4) Đường thẳng x = x 0 là đường tiệm cận đứng của đồ thị hàm số y = f(x) nếu lim x → x 0 + f x = - ∞ h o ặ c lim x → x 0 - f x = - ∞
Trong các mệnh đề trên, số mệnh đề đúng là:
A. 1
B. 2
C. 3
D. 4
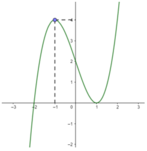
Cho hàm số f ( x ) = a x 4 + b x 2 - 1 ( a , b ∈ ℝ ) . Đồ thị của hàm số y=f(x) như hình vẽ bên. Số nghiệm thực của phương trình 2018.f(x) + 2019 = 0 là:
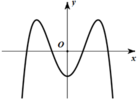
A. 4
B. 0
C. 3
D. 2
cho hàm số y=f(x) có f'(x) = (x-2021)^5 * (x-2020)^2020 * (x-2019)^2019. Hàm số f(x) có bao nhiêu điểm cực trị ?