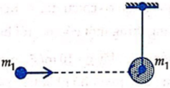
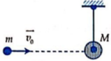
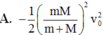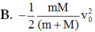Một viên đạn có khối lương m=50g bay theo phương ngang với vận tốc v0 đến cắm vào vật khối lượng M=450g đang đứng yên, được treo cố định bằng một sợi dây nhẹ không dãn có chiều dài l=1m. Coi vật va chạm là mềm. bỏ qua sức cản kk. Biết độ cao cực đại mà vật lên được so với vị trí ban đầu là h=50cm. lấy g=10m/s2
a, Tính vận tốc v của vật ngay sau khi va chạm và vo
b, Gia tốc của vật khi dây treo hợp với phương thẳng đứng 1 góc \(\alpha\)=45
Lấy mốc thế năng tại vị trí ban đầu của \(M\).
(a) Bảo toàn cơ năng cho hệ \(\left(m+M\right):\)
\(\dfrac{1}{2}\left(m+M\right)v^2=\left(m+M\right)gh\Rightarrow v=\sqrt{2gh}\)
\(\Rightarrow v=\sqrt{2\cdot10\cdot0,5}=\sqrt{10}\left(ms^{-1}\right)\)
Bảo toàn động lượng cho hệ theo phương ngang:
\(mv_0=\left(m+M\right)v\Rightarrow v_0=\dfrac{m+M}{m}v\)
\(\Rightarrow v_0=\dfrac{0,05+0,45}{0,05}\cdot\sqrt{10}=10\sqrt{10}\left(ms^{-1}\right)\)
(b) Bảo toàn cơ năng cho vật:
\(\dfrac{1}{2}mv^2=\dfrac{1}{2}mV^2+mgl\left(1-cos\alpha\right)\)
\(\Rightarrow V^2=v^2-2gl\left(1-cos\alpha\right)\)
Gia tốc hướng tâm: \(a_n=\dfrac{V^2}{l}=\dfrac{v^2-2gl\left(1-cos\alpha\right)}{l}\)
\(\Rightarrow a_n=\dfrac{\left(\sqrt{10}\right)^2-2\cdot10\cdot1\left(1-cos45^o\right)}{1}=10\sqrt{2}-10\left(ms^{-2}\right)\)
Gia tốc tiếp tuyến: \(a_t=gsin\alpha=10sin45^o=5\sqrt{2}\left(ms^{-2}\right)\)
Gia tốc của vật:
\(a=\sqrt{a_n^2+a_t^2}\approx8,19\left(ms^{-2}\right)\).