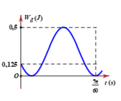
Góc quét được khi vật đi từ thời điểm ban đầu đến VTCB lần thứ 4 là:
\(\alpha=2\pi+\dfrac{\pi}{3}+\pi=\dfrac{10}{3}\pi\)
Thời điểm vật đi qua VTCB lần thứ 4 từ thời điểm ban đầu là:
\(t=\dfrac{\alpha}{\omega}=\dfrac{\dfrac{10}{3}\pi}{4\pi}=\dfrac{5}{6}\left(s\right)\)
Đ/S: \(\dfrac{5}{6}s\)
\(VTCB\Rightarrow x=0\Rightarrow cos\left(4\pi t+\dfrac{\pi}{6}\right)=0=cos\dfrac{\pi}{2}\Rightarrow4\pi t+\dfrac{\pi}{6}=\pm\dfrac{\pi}{2}\)
\(TH1:\) Vật qua \(x=0\) theo chiều âm, góc quét từ vị trí ban đầu\(\dfrac{\pi}{2}-\dfrac{\pi}{6}=\dfrac{\pi}{3}>0\) và từ vị trí này để đi đến \(VTCB\) lần thứ \(4\) phải quét thêm 1 góc \(2\pi\) (1 vòng tròn qua \(2\) \(VTCB\)), thời gian lúc đó là :
\(t=\dfrac{\varphi}{\omega}=\dfrac{\dfrac{\pi}{3}+2\pi}{4\pi}=\dfrac{7}{12}\approx0,6\left(s\right)\)
\(TH2:\) Vật qua \(x=0\) theo chiều dương, góc quét vị trí ban đầu \(\)\(-\dfrac{\pi}{2}-\dfrac{\pi}{6}=-\dfrac{2\pi}{3}< 0\), tương tự như trên ta có :
\(t=\dfrac{\varphi}{\omega}=\dfrac{-\dfrac{2\pi}{3}+2\pi}{4\pi}=\dfrac{1}{3}\approx0,3\left(s\right)\)