Đáp án C
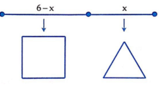
Cắt sợi dây 6 mét đã cho thành hai phần có độ dài lần luột là x mét và 6-x mét 0 < x < 6 . Phần thứ nhất có độ dài x mét được uốn thành hình tam giác đều cạnh bằng x 3 mét. Phần thứ hai có độ dài 6-x mét được uốn thành hình vuông cạnh bằng 6 − x 4 mét.
Diện tích phần I là S 1 = x 3 2 . 3 4 = x 2 3 36 m 2 .
Diện tích phần II là S 2 = 6 − x 4 2 m 2 .
Tổng diện tích hai phần là S x = S 1 + S 2 = x 2 3 36 + 6 − x 4 2 m 2 với x ∈ 0 ; 6
Đạo hàm S ' x = x 3 18 − 6 − x 8 ; S ' x = 0 ⇔ x = 54 9 + 4 3 ∈ 0 ; 6 . Lập bảng biến thiên của hàm số S x trên khoảng 0 ; 6 , ta thấy min S x = S 54 9 + 4 3 .
Khi đó cạnh của tam giác đều bằng 18 9 + 4 3 m .