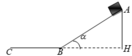
Một quả bóng rơi tự do từ độ cao h xuống một mặt phẳng nghiêng góc α so với mặt phẳng ngang. Sau khi va chạm tuyệt đối đàn hồi với mặt phẳng nghiêng, bóng tiếp tục nảy lên rồi lại và chạm vào mặt phẳng nghiêng và tiếp tục nảy lên, và cứ tiếp tục như thế. Giả sử mặt phẳng nghiêng đủ dài để quá trình va chạm của vật xảy ra liên tục. Khoảng cách giữa các điểm rơi liên tiếp kể từ lần thứ nhất đến lần thứ tư theo thứ tự lần lượt là l1, l2 và l3. Tìm hệ thức liên hệ giữa l1, l2 và l3.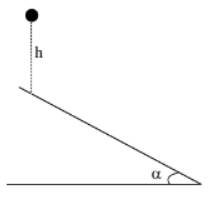
Đầu tiên, ta xác định các biến:
h: độ cao ban đầu của quả bóng (m)α: góc nghiêng của mặt phẳng nghiêng so với mặt phẳng ngang (đơn vị góc)v: vận tốc của quả bóng sau khi va chạm tại mỗi lần nảy lên (m/s)l1: khoảng cách giữa các điểm rơi liên tiếp từ lần thứ nhất đến lần thứ hai (m)l2: khoảng cách giữa các điểm rơi liên tiếp từ lần thứ hai đến lần thứ ba (m)l3: khoảng cách giữa các điểm rơi liên tiếp từ lần thứ ba đến lần thứ tư (m)Giả sử quả bóng rơi tự do từ độ cao h xuống mặt phẳng nghiêng. Khi va chạm tuyệt đối đàn hồi với mặt phẳng nghiêng, năng lượng và động lượng của quả bóng được bảo toàn.
Ta có công thức tính năng lượng và động lượng của quả bóng sau khi va chạm:
Năng lượng sau va chạm = Năng lượng trước va chạm (1/2)mv^2 = mgh
Động lượng sau va chạm = Động lượng trước va chạm mv = m√(2gh)
Trong đó: m: khối lượng của quả bóng (kg) g: gia tốc trọng trường (m/s^2)
Ở lần thứ nhất, quả bóng rơi từ độ cao h xuống mặt phẳng nghiêng, nên ta có: l1 = h*sin(α)
Ở lần thứ hai, quả bóng nảy lên từ mặt phẳng nghiêng, nên ta có: l2 = 2h*sin(α)*cos(α)
Ở lần thứ ba, quả bóng rơi từ độ cao h xuống mặt phẳng nghiêng, nên ta có: l3 = 2h*sin^2(α)*cos(α)
Vậy, hệ thức liên hệ giữa l1, l2 và l3 là: l1 = hsin(α) l2 = 2hsin(α)cos(α) l3 = 2hsin^2(α)*cos(α)