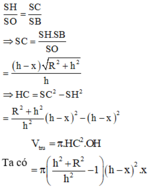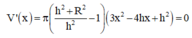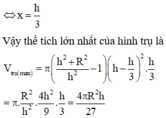Các câu hỏi tương tự
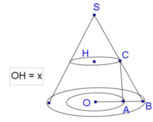
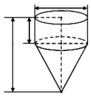
Một nóc tòa nhà cao tầng có dạng hình nón. Người ta muốn xây một bể nước có dạng một hình trụ nội tiếp trong hình nón để chứa nước (như hình vẽ minh họa). Cho biết
SO
h
;
OB
R
;
OH
x
0
x
h
.
Tìm thể tích lớn nhất của hình trụ. A.
2...
Đọc tiếp
Một nóc tòa nhà cao tầng có dạng hình nón. Người ta muốn xây một bể nước có dạng một hình trụ nội tiếp trong hình nón để chứa nước (như hình vẽ minh họa). Cho biết SO = h ; OB = R ; OH = x 0 < x < h . Tìm thể tích lớn nhất của hình trụ.
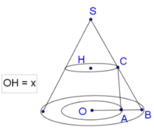
A. 2 πR 2 h 27
B. 2 πR 2 h 9
C. 4 πR 2 h 9
D. 4 πR 2 h 27
Cho tam giác SOA vuông tại O, có MN//SO với M, N lần lượt nằm trên cạnh SA,OA như hình vẽ bên. Đặt SO h không đổi. Khi quay hình vẽ quanh SO thì tạo thành một hình trụ nội tiếp hình nón đỉnh S có đáy là hình tròn tâm O, bán kính R OA. Tìm độ dài của MN theo h để thể tích khối trụ là lớn nhất A. MN h/2 B. MN h/3 C. MN h/4 D. MN h/6
Đọc tiếp
Cho tam giác SOA vuông tại O, có MN//SO với M, N lần lượt nằm trên cạnh SA,OA như hình vẽ bên. Đặt SO = h không đổi. Khi quay hình vẽ quanh SO thì tạo thành một hình trụ nội tiếp hình nón đỉnh S có đáy là hình tròn tâm O, bán kính R = OA. Tìm độ dài của MN theo h để thể tích khối trụ là lớn nhất
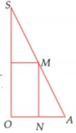
A. MN = h/2
B. MN = h/3
C. MN = h/4
D. MN = h/6
Cho tam giác SOA vuông tại O có MN//SO với M, N lần lượt nằm trên cạnh SA, OA như hình vẽ bên dưới. Đặt
S
O
h
không đổi. Khi quay hình vẽ quanh SO thì tạo thành một hình trụ nội tiếp hình nón đỉnh S có đáy là hình tròn tâm O bán kính
R
O
A
. Tìm độ dài của MN theo h để thể tích khối trụ là lớn nhất. A.
M
N
h
3
B...
Đọc tiếp
Cho tam giác SOA vuông tại O có MN//SO với M, N lần lượt nằm trên cạnh SA, OA như hình vẽ bên dưới. Đặt S O = h không đổi. Khi quay hình vẽ quanh SO thì tạo thành một hình trụ nội tiếp hình nón đỉnh S có đáy là hình tròn tâm O bán kính R = O A . Tìm độ dài của MN theo h để thể tích khối trụ là lớn nhất.
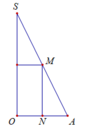
A. M N = h 3
B. M N = h 4
C. M N = h 6
D. M N = h 2
Cho tam giác SOA vuông tại O có MN//SO với M, N lần lượt nằm trên cạnh SA, OA như hình vẽ bên. Đặt SO h không đổi. Khi quay hình vẽ quanh SO thì tạo thành một hình trụ nội tiếp hình nón đỉnh S có đáy là hình tròn tâm O bán kính R OA. Tìm độ dài của MN theo h để thể tích khối trụ là lớn nhất A.
M
N
h
2
B.
M
N
h
3
C.
M
N...
Đọc tiếp
Cho tam giác SOA vuông tại O có MN//SO với M, N lần lượt nằm trên cạnh SA, OA như hình vẽ bên. Đặt SO = h không đổi. Khi quay hình vẽ quanh SO thì tạo thành một hình trụ nội tiếp hình nón đỉnh S có đáy là hình tròn tâm O bán kính R = OA. Tìm độ dài của MN theo h để thể tích khối trụ là lớn nhất
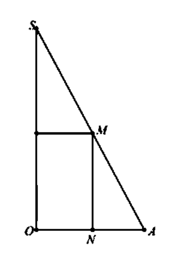
A. M N = h 2
B. M N = h 3
C. M N = h 4
D. M N = h 6
Một cái nắp của bình chứa rượu gồm một phần dạng hình trụ, phần còn lại có dạng nón (như hình vẽ). Phần hình nón có bán kính đáy là r, chiều cao là h, đường sinh bằng 1,25m. Phần hình trụ có bán kính bằng bán kính đáy của hình nón, chiều cao bằng
h
3
. Kết quả
r
+
h
xấp xỉ bằng bao nhiêu cen-ti-mét để diện tích toàn phần cái nắp là lớn nhất. A. 427 B. 381 C. 348 D. 299
Đọc tiếp
Một cái nắp của bình chứa rượu gồm một phần dạng hình trụ, phần còn lại có dạng nón (như hình vẽ). Phần hình nón có bán kính đáy là r, chiều cao là h, đường sinh bằng 1,25m. Phần hình trụ có bán kính bằng bán kính đáy của hình nón, chiều cao bằng h 3 . Kết quả r + h xấp xỉ bằng bao nhiêu cen-ti-mét để diện tích toàn phần cái nắp là lớn nhất.
A. 427
B. 381
C. 348
D. 299
Để tiết kiệm vật liệu nhất thì
S
t
p
nhỏ nhất
⇔
πR
2
π
R
⇒
R
1
⇒
h
2
Cho đồ thị hàm số yf(x) như hình vẽ dưới đây: Có bao nhiêu giá trị nguyên dương của tham số m để hàm số
y
f
(
x...
Đọc tiếp
Để tiết kiệm vật liệu nhất thì S t p nhỏ nhất ⇔ πR 2 = π R ⇒ R = 1 ⇒ h = 2 Cho đồ thị hàm số y=f(x) như hình vẽ dưới đây:
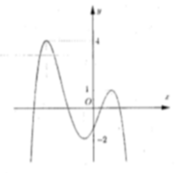
Có bao nhiêu giá trị nguyên dương của tham số m để hàm số y = f ( x - 2 ) - m 4 có 7 điểm cực trị.
A. 1
B. 2
C. 3
D. 4
Cho hình nón có chiều cao h. Một hình trụ nối tiếp bên trong hình nón có chiều cao x thay đổi. Tính chiều cao x của hình trụ theo h sao cho thể tích của khối trụ sinh bởi hình trụ đó là lớn nhất A.
x
h
2
B.
x
h
3
C.
x
2
h
3
D.
x
h...
Đọc tiếp
Cho hình nón có chiều cao h. Một hình trụ nối tiếp bên trong hình nón có chiều cao x thay đổi. Tính chiều cao x của hình trụ theo h sao cho thể tích của khối trụ sinh bởi hình trụ đó là lớn nhất
A. x = h 2
B. x = h 3
C. x = 2 h 3
D. x = h 3
Cho hình nón có chiều cao h. Tính chiều cao x của khối trụ có thể tích lớn nhất nội tiếp trong hình nón theo h. A.
x
h
2
.
B.
x
h
3
.
C.
x
2
h
3
.
D.
x
h
3
.
Đọc tiếp
Cho hình nón có chiều cao h. Tính chiều cao x của khối trụ có thể tích lớn nhất nội tiếp trong hình nón theo h.
A. x = h 2 .
B. x = h 3 .
C. x = 2 h 3 .
D. x = h 3 .
Cho hình nón có chiều cao h. Tính chiều cao x của khối trụ có thể tích lớn nhất nội tiếp trong hình nón theo h
Đọc tiếp
Cho hình nón có chiều cao h. Tính chiều cao x của khối trụ có thể tích lớn nhất nội tiếp trong hình nón theo h
![]()
![]()
![]()
![]()