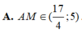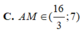Một người xây nhà xưởng hình hộp chữ nhật có diện tích mặt sàn là 1152 m 2 và chiều cao cố định. Người đó xây các bức tường xung quanh và bên trong để ngăn nhà xưởng thành ba phòng hình chữ nhật có kích thước như nhau (không kể trần nhà). Vậy cần phải xây các phòng theo kích thước nào để tiết kiệm chi phí nhất (bỏ qua độ dày các bức tường).
A. 16m x 24m
B. 8m x 48m
C. 12m x 32m
D. 24m x 32m
Đáp án D
Đặt x, y, h lần lượt là chiều dài, chiều rộng và chiều cao mỗi phòng.
Theo giả thiết, ta có x.3y = 1152 → y = 384 x
Để tiết kiệm chi phí nhất khi diện tích toàn phần nhỏ nhất.
Ta có ![]()
![]()
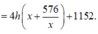
Vì h không đổi nên
S
t
p
nhỏ nhất khi ![]() (với x > 0) nhỏ nhất.
(với x > 0) nhỏ nhất.
Khảo sát ![]() với x > 0 ta được f(x) nhỏ nhất khi x = 24 => y = 16
với x > 0 ta được f(x) nhỏ nhất khi x = 24 => y = 16