Một người đi ngựa và một người đi bộ đều đi từ bản A đến bản B. Người đi ngựa đến B trước người đi bộ 50 phút rồi lập tức quay trở về A và gặp người đi bộ tại một địa điểm cách B là 2km. Trên cả quãng đường từ A đến B và ngược lại, người đi ngựa đi hết 1 giờ 40 phút. Hãy tính khoảng cách AB và vận tốc của mỗi người.
Giả sử khoảng cách AB = d (km).
Gọi vận tốc của người đi bộ là x km/h, x > 0.
Theo đầu bài, người đi ngựa đi quãng đường AB hết 5/6 giờ. Do đó vận tốc của người đi ngựa là d: 5/6 = 6d/5 (km).
Người đi ngựa đến trước người đi bộ 5/6 giờ. Điều đó có nghĩa là
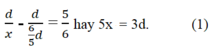
Từ đó cũng suy ra 6d/5 = 2x; nghĩa là vận tốc của người đi ngựa là 2x km/h. Vì người đi ngựa khi quay lại gặp người đi bộ ở điểm cách B một khoảng là 2km nên:
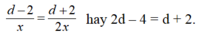
Từ (1) và (2), ta có hệ phương trình 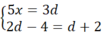
Giải hệ này ta được d = 6, x = 3,6.
Vậy: Khoảng cách AB = d = 6 km,
Vận tốc của người đi bộ là 3,6 km/h,
Vận tốc của người đi ngựa là 7,2 km/h.

