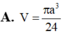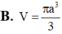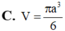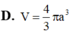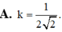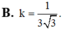Các câu hỏi tương tự
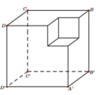
Một khối đa diện (H) được tạo thành bằng cách từ một khối lập phương cạnh bằng 3, ta bỏ đi khối lập phương cạnh bằng 1 ở một “góc” của nó như hình vẽ. Gọi (S) là khối cầu có thể tích lớn nhất chứa trong (H) và tiếp xúc với các mặt Tính bán kính của (S).
Đọc tiếp
Một khối đa diện (H) được tạo thành bằng cách từ một khối lập phương cạnh bằng 3, ta bỏ đi khối lập phương cạnh bằng 1 ở một “góc” của nó như hình vẽ. Gọi (S) là khối cầu có thể tích lớn nhất chứa trong (H) và tiếp xúc với các mặt ![]() Tính bán kính của (S).
Tính bán kính của (S).
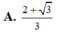
![]()

![]()
Một hình lập phương có cạnh bằng 2a vừa nội tiếp hình trụ (T) vừa nội tiếp mặt cầu (C) và hai đáy của hình lập phương nằm trên 2 đáy của hình trụ. Tính tỉ số thể tích
V
c
V
T
giữa khối cầu và khối trụ giới hạn bởi (C) và (T) ?
Đọc tiếp
Một hình lập phương có cạnh bằng 2a vừa nội tiếp hình trụ (T) vừa nội tiếp mặt cầu (C) và hai đáy của hình lập phương nằm trên 2 đáy của hình trụ. Tính tỉ số thể tích V c V T giữa khối cầu và khối trụ giới hạn bởi (C) và (T) ?
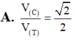
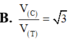
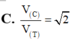
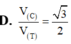
Cho khối nón có góc ở đỉnh của thiết diện qua trục là
π
3
. Một khối cầu (S1) nội tiếp trong khối nón. Gọi S2 là khối cầu tiếp xúc với tất cả các đường sinh của nón và với S1; S3 là khối tiếp xúc với tất cả các đường sinh của nón và với S2; ….; Sn là khối cầu tiếp xúc với tất cả các đường sinh của nón và với Sn-1. Gọi V1, V2, V3, … , Vn-1, Vn lần lượt là thể tích của khối cầu S1, S2, S3, …, Sn-1, Sn và V là thể tích của khối nón. Tính giá trị biểu thức...
Đọc tiếp
Cho khối nón có góc ở đỉnh của thiết diện qua trục là π 3 . Một khối cầu (S1) nội tiếp trong khối nón. Gọi S2 là khối cầu tiếp xúc với tất cả các đường sinh của nón và với S1; S3 là khối tiếp xúc với tất cả các đường sinh của nón và với S2; ….; Sn là khối cầu tiếp xúc với tất cả các đường sinh của nón và với Sn-1. Gọi V1, V2, V3, … , Vn-1, Vn lần lượt là thể tích của khối cầu S1, S2, S3, …, Sn-1, Sn và V là thể tích của khối nón. Tính giá trị biểu thức T = l i m n → + ∞ = V 1 + V 2 + . . . + V n V
![]()
![]()
![]()
![]()
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh bằng 1, mặt bên SAB là tam giác cân tại S và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính thể tích V của khối cầu ngoại tiếp hình chóp đã cho biết
A
S
B
^
120
0
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh bằng 1, mặt bên SAB là tam giác cân tại S và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính thể tích V của khối cầu ngoại tiếp hình chóp đã cho biết A S B ^ = 120 0
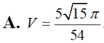
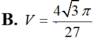
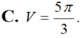
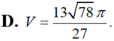
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh bằng 1, mặt bên SAB là tam giác cân tại S và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính thể tích V của khối cầu ngoại tiếp hình chóp đã cho biết
A
S
B
^
120
0
A.
V
5
15...
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh bằng 1, mặt bên SAB là tam giác cân tại S và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính thể tích V của khối cầu ngoại tiếp hình chóp đã cho biết A S B ^ = 120 0
A. V = 5 15 π 54
B. V = 4 3 π 27
C. V = 5 π 3
D. V = 13 78 π 27
Cho hình chóp S.ABC có đáy là tam giác vuông cân tại B, ABd. Cạnh bên SA vuông góc với mặt phẳng (ABC) và SC hợp với đáy một góc bằng 60°. Gọi (S) là mặt cầu ngoại tiếp khối chóp S.ABC. Tính thể tích khối cầu (S).
Đọc tiếp
Cho hình chóp S.ABC có đáy là tam giác vuông cân tại B, AB=d. Cạnh bên SA vuông góc với mặt phẳng (ABC) và SC hợp với đáy một góc bằng 60°. Gọi (S) là mặt cầu ngoại tiếp khối chóp S.ABC. Tính thể tích khối cầu (S).
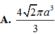
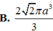
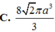
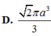
Cho tứ diện ABCD có
A
D
⊥
(
A
B
C
)
, đáy ABC thỏa mãn điều kiện Gọi H, K lần lượt là hình chiếu vuông góc của A lên DB và DC. Tính thể tích V của khối cầu ngoại tiếp khối chóp A. BCHK. A.
32
π
3
B.
8
π
3...
Đọc tiếp
Cho tứ diện ABCD có
A
D
⊥
(
A
B
C
)
, đáy ABC thỏa mãn điều kiện 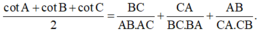
Gọi H, K lần lượt là hình chiếu vuông góc của A lên DB và DC.
Tính thể tích V của khối cầu ngoại tiếp khối chóp A. BCHK.
A. 32 π 3
B. 8 π 3
C. 4 π 3 3
D. 4 π 3
Cho hình chóp đều S.ABC có cạnh đáy bằng a, cạnh bên hợp với mặt đáy một góc
60
o
Gọi (S ) là mặt cầu ngoại tiếp hình chóp S.ABC. Thể tích của khối cầu tạo nên bởi mặt cầu (S ) bằng
Đọc tiếp
Cho hình chóp đều S.ABC có cạnh đáy bằng a, cạnh bên hợp với mặt đáy một góc 60 o Gọi (S ) là mặt cầu ngoại tiếp hình chóp S.ABC. Thể tích của khối cầu tạo nên bởi mặt cầu (S ) bằng
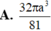
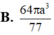
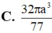
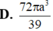
Trong không gian mặt cầu (S) tiếp xúc với 6 mặt của một hình lập phương cạnh a, thể tích khối cầu (S)bằng
Đọc tiếp
Trong không gian mặt cầu (S) tiếp xúc với 6 mặt của một hình lập phương cạnh a, thể tích khối cầu (S)bằng