Đáp án D
Hình chóp có 10 cạnh thì tức là hình chóp có đáy có 10 2 = 5 cạnh. Tức là đáy có 5 điểm ở đáy kết hợp với 1 đỉnh, vậy hình chóp này có 6 điểm.
Đáp án D
Hình chóp có 10 cạnh thì tức là hình chóp có đáy có 10 2 = 5 cạnh. Tức là đáy có 5 điểm ở đáy kết hợp với 1 đỉnh, vậy hình chóp này có 6 điểm.
Một hình chóp có tất cả 10 cạnh. Số mặt của hình chóp đó bằng
A.6.
B.7.
C.4.
D.5
Cho hình chóp có đáy là một đa giác chín cạnh. Tất cả các cạnh bên và đường chéo của đa giác đáy được bôi bởi một trong hai màu đỏ hoặc xanh. Chứng minh rằng tồn tại ba đỉnh của hình chóp sao cho chúng là những đỉnh của của hình tam giác với các cạnh được bôi cùng màu.
Cho hình chóp tứ giác đều S. ABCD, có cạnh đáy bằng a và có thể tích a 3 3 6 Gọi J là điểm cách đều tất cả các mặt của hình chóp. Tính khoảng cách d từ J đến mặt phẳng đáy
A. d = a 3 4
B. d = a 3 2
C. d = a 3 6
D. d = a 3 3
Câu 9. Cho hình chóp S.ABCD có tất cả các cạnh bằng a. Gọi I, J lần lượt là trọng tâm của tam giác SAD, SBC . Mặt phẳng (BIJ) cắt hình chóp theo một thiết diện. Diện tích thiết diện đó là:
Trong tất cả các hình chóp tứ giác đều có d= 3 là khoảng cách giữa hai đường thẳng chéo nhau gồm một đường thẳng chứa một đường chéo của đáy và đường thẳng còn lại chứa một cạnh bên hình chóp. Thể tích nhỏ nhất V m i n của khối chóp là
A. V m i n =3
B. V m i n =9
C. V m i n = 9 3
D. V m i n =27
Cho hình chóp S.ABCD có cạnh SA = x còn tất cả các cạnh khác có độ dài bằng 2. Tính thể tích lớn nhất của khối chóp S.ABCD
A. V = 1
B. V = 1 2
C. V = 3
D. V = 2
Cho hình chóp tứ giác đều có tất cả các cạnh đều bằng a. Tính cosin của góc giữa một mặt bên và một mặt đáy.
A. 1 2
B. 1 3
C. 1 3
D. 1 2
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, tất cả các cạnh bên tạo với mặt phẳng đáy một góc 60 o . Thể tích của khối chóp S.ABCD là



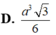
Cho hình chóp có 20 cạnh. Tính số mặt của hình chóp đó.
A. 20
B. 11
C. 12
D. 10