Các câu hỏi tương tự
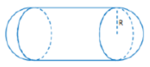
Một cái bổn chứa nước gổm hai nửa hình cầu và một hình trụ(như hình vẽ). Đường sinh của hình trụ bằng hai lần đường kính của hình cầu. Biết thể tích của bồn chứa nước là
128
π
3
(
m
3
)
Tính diện tích xung quanh của cái bồn chứa nước theo đơn vị
m
3
. A. 50...
Đọc tiếp
Một cái bổn chứa nước gổm hai nửa hình cầu và một hình trụ(như hình vẽ). Đường sinh của hình trụ bằng hai lần đường kính của hình cầu. Biết thể tích của bồn chứa nước là 128 π 3 ( m 3 ) Tính diện tích xung quanh của cái bồn chứa nước theo đơn vị m 3 .
A. 50 π 2 ( m 2 )
B. 64 π 2 ( m 2 )
C. 40 π 2 ( m 2 )
D. 48 π 2 ( m 2 )
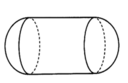
Mọt cái bồn chứa xăng gồm hai nửa hình cầu và một hình trụ (như hình vẽ). Các kích thước được ghi cùng đơn vị. Hãy tính thể tích của bồn chứa A.
π
4
2
.
3
5
B.
π
4
5
.
3
2
C.
π
4
2...
Đọc tiếp
Mọt cái bồn chứa xăng gồm hai nửa hình cầu và một hình trụ (như hình vẽ). Các kích thước được ghi cùng đơn vị. Hãy tính thể tích của bồn chứa
A. π 4 2 . 3 5
B. π 4 5 . 3 2
C. π 4 2 3 5
D. π 4 5 3 2
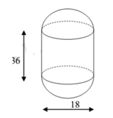
Một cái bồn gồm hai nửa hình cầu đường kính 18dm và một hình trụ có chiều cao 36dm (như hình vẽ). Tính thể tích V của cái bồn đó A. V 9216
π
dm
3
B. V
1024
π
9
d
m
3
C. V
16
π
243
...
Đọc tiếp
Một cái bồn gồm hai nửa hình cầu đường kính 18dm và một hình trụ có chiều cao 36dm (như hình vẽ). Tính thể tích V của cái bồn đó
A. V = 9216 π dm 3
B. V = 1024 π 9 d m 3
C. V = 16 π 243 d m 3
D. V = 3888 d m 3
Trên bàn có một cốc nước hình trụ chứa đầy nước, có chiều cao bằng 3 lần đường kính của đáy; một viên bi và một khối nón đều bằng thủy tinh. Biết viên bi là một khối cầu có đường kính bằng đường kính của cốc nước. Người ta từ từ thả vào cốc nước viên bi và khối nón đó (như hình vẽ) thì thấy nước trong cốc tràn ra ngoài. Tính tỉ số thể tích của lượng nước còn lại trong cốc và lượng nước ban đầu (bỏ qua bề dày của lớp vỏ thủy tinh).
Đọc tiếp
Trên bàn có một cốc nước hình trụ chứa đầy nước, có chiều cao bằng 3 lần đường kính của đáy; một viên bi và một khối nón đều bằng thủy tinh. Biết viên bi là một khối cầu có đường kính bằng đường kính của cốc nước. Người ta từ từ thả vào cốc nước viên bi và khối nón đó (như hình vẽ) thì thấy nước trong cốc tràn ra ngoài. Tính tỉ số thể tích của lượng nước còn lại trong cốc và lượng nước ban đầu (bỏ qua bề dày của lớp vỏ thủy tinh).

![]()
![]()
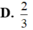
Một hình trụ có tâm các đáy là A,B. Biết rằng mặt cầu đường kính AB tiếp xúc với các mặt, đáy của hình trụ tại A,B và tiếp xúc với mặt xung quanh của hình trụ đó. Diện tích của mặt cầu này là
16
π
. Tính diện tích xung quanh của mặt trụ đã cho.
A
.
16
π
3
B
.
16
π
C
.
8...
Đọc tiếp
Một hình trụ có tâm các đáy là A,B. Biết rằng mặt cầu đường kính AB tiếp xúc với các mặt, đáy của hình trụ tại A,B và tiếp xúc với mặt xung quanh của hình trụ đó. Diện tích của mặt cầu này là 16 π . Tính diện tích xung quanh của mặt trụ đã cho.
A . 16 π 3
B . 16 π
C . 8 π
D . 8 π 3
Cho hình trụ (T) có bán kính bằng 4cm mặt phẳng (P) cắt hai đáy của hình trụ theo hai dây AB và CD, ABCD5cm Tứ giác ABCD là hình chữ nhật AD và BC không là đường sinh,góc giữa mp (P) và mặt phẳng chứa đáy của hình trụ bằng
60
o
Thể tích của khối trụ là:
Đọc tiếp
Cho hình trụ (T) có bán kính bằng 4cm mặt phẳng (P) cắt hai đáy của hình trụ theo hai dây AB và CD, AB=CD=5cm Tứ giác ABCD là hình chữ nhật AD và BC không là đường sinh,góc giữa mp (P) và mặt phẳng chứa đáy của hình trụ bằng 60 o Thể tích của khối trụ là:
![]()
![]()
![]()
![]()
Cho hình trụ (T) có diện tích đáy bằng 48π và hai dây cung AB,CD lần lượt nằm trên hai đường tròn đáy của (T) sao cho ABCD là một hình vuông có độ dài cạnh bằng 10 và các cạnh của hình vuông này không song song với đường sinh của (T) (tham khảo hình vẽ bên). Tính thể tích của khối trụ (T). A. 288π B.
96
2
π C.
192...
Đọc tiếp
Cho hình trụ (T) có diện tích đáy bằng 48π và hai dây cung AB,CD lần lượt nằm trên hai đường tròn đáy của (T) sao cho ABCD là một hình vuông có độ dài cạnh bằng 10 và các cạnh của hình vuông này không song song với đường sinh của (T) (tham khảo hình vẽ bên). Tính thể tích của khối trụ (T).
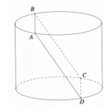
A. 288π
B. 96 2 π
C. 192 2 π.
D. 384π
Khi cắt mặt cầu S (O; R) bởi một mặt kính đi qua tâm O, ta được hai nửa mặt cầu giống nhau. Giao tuyến của mặt kính đó với mặt cầu gọi là mặt đáy của mỗi nửa mặt cầu. Một hình trụ gọi là nội tiếp nửa mặt cầu S (O; R) nếu một đáy của hình trụ nằm trong đáy của nửa mặt cầu, còn đường tròn đáy kia là giao tuyến của hình trụ với nửa mặt cầu. Biết R 1, tính bán kính đáy r và chiều cao h của hình trụ nội tiếp nửa mặt cầu S(O; R) để khối trụ có thể tích lớn nhất.
Đọc tiếp
Khi cắt mặt cầu S (O; R) bởi một mặt kính đi qua tâm O, ta được hai nửa mặt cầu giống nhau. Giao tuyến của mặt kính đó với mặt cầu gọi là mặt đáy của mỗi nửa mặt cầu. Một hình trụ gọi là nội tiếp nửa mặt cầu S (O; R) nếu một đáy của hình trụ nằm trong đáy của nửa mặt cầu, còn đường tròn đáy kia là giao tuyến của hình trụ với nửa mặt cầu. Biết R = 1, tính bán kính đáy r và chiều cao h của hình trụ nội tiếp nửa mặt cầu S(O; R) để khối trụ có thể tích lớn nhất.
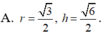


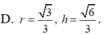
Cho hình trụ có diện tích xung quanh bằng 16
π
a
2
và độ dài đường sinh bằng 2a. Tính bán kính r của đường tròn đáy của hình trụ đã cho. A. r 4a B.r 6a. C.r 4
π
. D. r 8a.
Đọc tiếp
Cho hình trụ có diện tích xung quanh bằng 16 π a 2 và độ dài đường sinh bằng 2a. Tính bán kính r của đường tròn đáy của hình trụ đã cho.
A. r = 4a
B.r = 6a.
C.r = 4 π .
D. r = 8a.
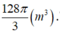 .Tính diện tích xung quanh của cái bồn chứa nước theo đơn vị
m
2
.Tính diện tích xung quanh của cái bồn chứa nước theo đơn vị
m
2