\(f\left(x\right)=x^2-\left(2m-1\right)x-2\sqrt{x}+m^2-2m\)
1) đk: \(x\ge0\)
Thay m=2 vào \(f\left(x\right)=0\) ta được: \(x^2-3x-2\sqrt{x}=0\)
\(\Leftrightarrow\)\(\sqrt{x}\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)^2=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x}=0\\\sqrt{x}-2=0\\\sqrt{x}+1=0\left(vn\right)\end{matrix}\right.\)\(\Leftrightarrow\)\(\left[{}\begin{matrix}x=0\\x=4\end{matrix}\right.\)(tm)
2) Thay m=6 vào f(x) ta được:
\(f\left(x\right)=x^2-11x-2\sqrt{x}+24\)
\(f\left(x\right)\le0\) \(\Leftrightarrow x^2-11x-2\sqrt{x}+24\le0\) (bước này coi \(\sqrt{x}\) là nghiệm thì sẽ trở thành bpt
bậc 4 ,bấm máy tính sẽ tìm được nghiệm)
\(\Leftrightarrow\)\(\left(\sqrt{x}-3\right)\left(\sqrt{x}+2\right)\left(\sqrt{x}-\dfrac{-1+\sqrt{17}}{2}\right)\left(\sqrt{x}+\dfrac{1+\sqrt{17}}{2}\right)\le0\)
mà \(\sqrt{x}\ge0\) \(\Rightarrow\left\{{}\begin{matrix}\sqrt{x}+2>0\\\sqrt{x}+\dfrac{1+\sqrt{17}}{2}>0\end{matrix}\right.\)
bpt \(\Leftrightarrow\left(\sqrt{x}-3\right)\left(\sqrt{x}-\dfrac{-1+\sqrt{17}}{2}\right)\le0\)
\(\Leftrightarrow\sqrt{x}\in\left[\dfrac{-1+\sqrt{17}}{2};3\right]\)
\(\Leftrightarrow x\in\left[\dfrac{9-\sqrt{17}}{2};9\right]\)











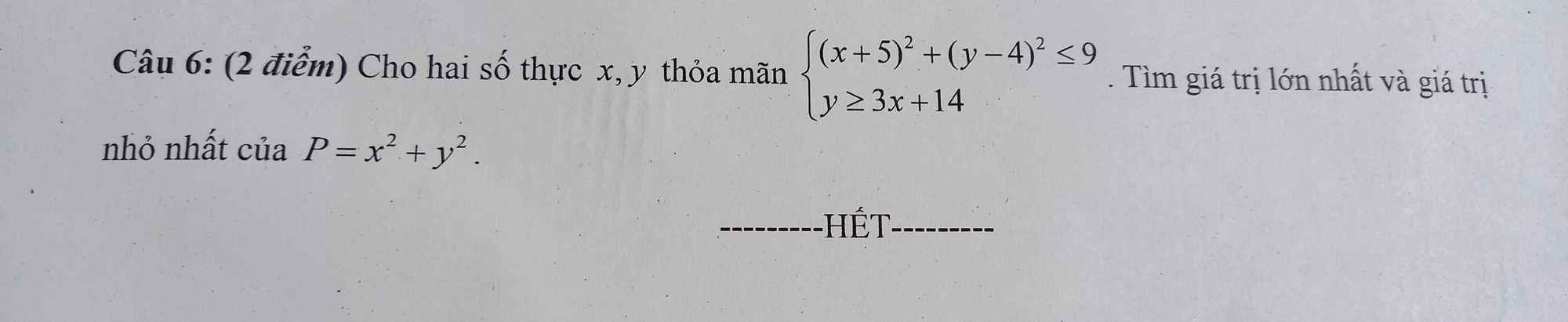




 mn giúp mình bài 3 vs ạ. Mình cảm ơn nhiều
mn giúp mình bài 3 vs ạ. Mình cảm ơn nhiều