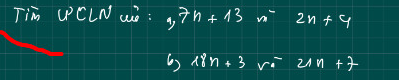a) -Đặt ƯCLN(\(7n+13;2n+4\))=a
=>\(\left(7n+13\right)⋮a\) ; \(\left(2n+4\right)⋮a\)
=>\(\left(7n+13\right)⋮a\) ; \(\left(n+2\right)⋮a\)
=>\(\left(7n+13\right)⋮a\) ; \(\left(7n+14\right)⋮a\)
=>\(\left[\left(7n+14\right)-\left(7n+13\right)\right]⋮a\)
=>\(1⋮a\)
=>\(a=1\).
-Vậy ƯCLN của \(7n+13;2n+4\) là 1.
b) -Đặt ƯCLN(\(18n+3;21n+7\))=b
=>\(\left(18n+3\right)⋮b\) ; \(\left(21n+7\right)⋮b\)
=>\(\left(6n+1\right)⋮b\) ; \(\left(3n+1\right)⋮b\)
=>\(\left(6n+1\right)⋮b\) ; \(\left(6n+2\right)⋮b\).
=>\(\left[\left(6n+2\right)-\left(6n+1\right)\right]⋮b\)
=>\(1⋮b\)
=>\(b=1\)
-Vậy ƯCLN của\(18n+3;21n+7\) là 1.