\(\frac{a}{b+c+d}=\frac{b}{c+d+a}=\frac{c}{d+a+b}=\frac{d}{a+b+c}\)
\(\Leftrightarrow\frac{a}{b+c+d}+1=\frac{b}{c+d+a}+1=\frac{c}{d+a+b}+1=\frac{d}{a+b+c}+1\)
\(\Leftrightarrow\frac{a+b+c+d}{b+c+d}=\frac{a+b+c+d}{c+d+a}=\frac{a+b+c+d}{d+a+b}=\frac{a+b+c+d}{a+b+c}\)
\(\Leftrightarrow\orbr{\begin{cases}a+b+c+d=0\\b+c+d=c+d+a=d+a+b=a+b+c\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}a+b+c+d=0\\a=b=c=d\end{cases}}\)
Với \(a+b+c+d=0\):
\(M=\frac{a+b}{c+d}+\frac{b+c}{d+a}+\frac{c+d}{a+b}+\frac{d+a}{b+c}\)
\(=\frac{-\left(c+d\right)}{c+d}+\frac{-\left(d+a\right)}{d+a}+\frac{-\left(a+b\right)}{a+b}+\frac{-\left(b+c\right)}{b+c}\)
\(=-1-1-1-1=-4\)
Nếu \(a=b=c=d\):
\(M=\frac{a+b}{c+d}+\frac{b+c}{d+a}+\frac{c+d}{a+b}+\frac{d+a}{b+c}=1+1+1+1=4\)
có bài j đâu
Hình ở trên ý



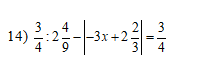 mọi người ơi giúp mình câu này với mình hứa sẽ kích đúng
mọi người ơi giúp mình câu này với mình hứa sẽ kích đúng