Đáp án là D
Theo tích chất hình đa diện thì mỗi đỉnh của hình da diện là đỉnh chung của ít nhất ba mặt
Đúng 0
Bình luận (0)
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Các câu hỏi tương tự
Mỗi đỉnh của hình đa diện là đỉnh chung của ít nhất bao nhiêu mặt?
A. Năm mặt.
B. Bốn mặt.
C. Ba mặt.
D. Hai mặt.
Gọi số đỉnh, số cạnh, số mặt của hình đa diện trong hình vẽ bên lần lượt là a, b, c. Hỏi T = a + b - c bằng bao nhiêu?
A. T = 10
B. T = 14
C. T = 38
D. T = 22
Cho khối đa diện (H) có các đỉnh là tâm các mặt bên của một hình lập phương có cạnh bằng 4. Xét hình nón tròn xoay (N) đi qua tất cả các đỉnh của đa diện (H), đỉnh và tâm đáy của (N) lần lượt là hai đỉnh của đa diện (H) nằm trên hai mặt bên đối lập nhau của hình lập phương (hình vẽ). Thể tích V của khối nón tròn xoay (N) bằng A.
256
π
B.
64
π
C.
64
π
3
D. ...
Đọc tiếp
Cho khối đa diện (H) có các đỉnh là tâm các mặt bên của một hình lập phương có cạnh bằng 4. Xét hình nón tròn xoay (N) đi qua tất cả các đỉnh của đa diện (H), đỉnh và tâm đáy của (N) lần lượt là hai đỉnh của đa diện (H) nằm trên hai mặt bên đối lập nhau của hình lập phương (hình vẽ). Thể tích V của khối nón tròn xoay (N) bằng
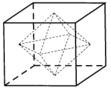
A. 256 π
B. 64 π
C. 64 π 3
D. 16 π 3
Chứng minh rằng một đa diện mà mỗi đỉnh của nó đều là đỉnh chung của số lẻ mặt thì tổng số các đỉnh của nó là một số chẵn. Cho ví dụ.
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, và SA vuông góc với mặt phẳng (ABCD). Góc giữa hai mặt phẳng (SBD) và (ABCD) bằng
45
°
. Gọi M là điểm đối xứng của C qua B và N là trung điểm của SC. Mặt phẳng (MND) chia khối chóp S.ABCD thành hai khối đa diện, trong đó khối đa diện chứa đỉnh S có thể tích
V
1
khối đa diện còn lại có thể tích
V
2
(tham khảo hình vẽ bên đây). T...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, và SA vuông góc với mặt phẳng (ABCD). Góc giữa hai mặt phẳng (SBD) và (ABCD) bằng 45 ° . Gọi M là điểm đối xứng của C qua B và N là trung điểm của SC. Mặt phẳng (MND) chia khối chóp S.ABCD thành hai khối đa diện, trong đó khối đa diện chứa đỉnh S có thể tích V 1 khối đa diện còn lại có thể tích V 2 (tham khảo hình vẽ bên đây). Tính tỉ số V 1 V 2
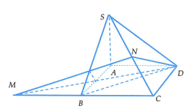
A. V 1 V 2 = 12 7
B. V 1 V 2 = 5 3
C. V 1 V 2 = 1 5
D. V 1 V 2 = 7 5
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh
a
,
B
A
D
⏜
60
0
và SA vuông góc với mặt phẳng
A
B
C
D
. Góc giữa hai mặt ph...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a , B A D ⏜ = 60 0 và SA vuông góc với mặt phẳng A B C D . Góc giữa hai mặt phẳng S B D và A B C D bằng 45 0 . Gọi M là điểm đối xứng của C qua B và N là trung điểm của SC. Mặt phẳng M N D chia khối chóp S.ABCD thành hai khối đa diện, trong đó khối đa diện chứa đỉnh S có thể tích V 1 và khối đa diện còn lại có thể tích bằng V 2 . Tính tỉ số V 1 V 2
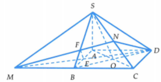
A. V 1 V 2 = 12 7
B. V 1 V 2 = 5 3
C. V 1 V 2 = 1 5
D. V 1 V 2 = 7 5
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a,
B
A
D
^
60
°
và SA vuông góc với mặt phẳng (ABCD). Góc giữa 2 mặt phẳng (SBD) và (ABCD) bằng 450. Gọi M là điểm đối xứng của C qua B và N là trung điểm của SC. Mặt phẳng (MND) chia khối chóp S.ABCD thành hai khối đa diện, trong đó khối đa diện chứa đỉnh S có thể tích V1, khối đa diện còn lại có thể tích V2 (tham khảo hình vẽ...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, B A D ^ = 60 ° và SA vuông góc với mặt phẳng (ABCD). Góc giữa 2 mặt phẳng (SBD) và (ABCD) bằng 450. Gọi M là điểm đối xứng của C qua B và N là trung điểm của SC. Mặt phẳng (MND) chia khối chóp S.ABCD thành hai khối đa diện, trong đó khối đa diện chứa đỉnh S có thể tích V1, khối đa diện còn lại có thể tích V2 (tham khảo hình vẽ bên). Tính tỉ số V 1 V 2
A. V 1 V 2 = 12 7
B. V 1 V 2 = 5 3
C. V 1 V 2 = 1 5
D. V 1 V 2 = 7 5
Cho hình chóp S.ABC có ABC là tam giác mà
A
B
1
,
A
C
2
,
B
A
C
^
60
∘
; SA vuông góc với mặt phẳng (ABC). Gọi
B
1
,
C
1
là hình chiếu của A lên SB, SC. Tính diện tích mặt cầu đi qua bốn đỉnh...
Đọc tiếp
Cho hình chóp S.ABC có ABC là tam giác mà A B = 1 , A C = 2 , B A C ^ = 60 ∘ ; SA vuông góc với mặt phẳng (ABC). Gọi B 1 , C 1 là hình chiếu của A lên SB, SC. Tính diện tích mặt cầu đi qua bốn đỉnh A , B , C , B 1 , C 1 ?
A. 8 π
B. 4 π
C. 16 π
D. 12 π
Trong một hình đa diện lồi, mỗi cạnh là cạnh chung của tất cả bao nhiêu mặt?
A. 5
B. 3
C. 4
D. 2