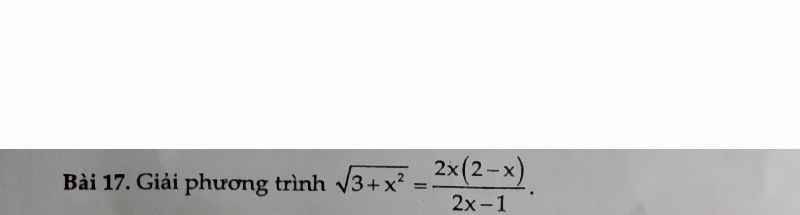ĐKXĐ:\(x\ne\dfrac{1}{2}\)
PT đã cho tương đương với:
\(\sqrt{3+x^2}-2=\dfrac{2x\left(2-x\right)}{2x-1}-2\)
\(\Leftrightarrow\dfrac{x^2-1}{\sqrt{3+x^2}+2}=2\left[\dfrac{x\left(2-x\right)}{2x-1}-1\right]\)
\(\Leftrightarrow\dfrac{x^2-1}{\sqrt{3+x^2}+2}+\dfrac{2\left(x^2-1\right)}{2x-1}=0\)
\(\Leftrightarrow\left(x^2-1\right)\left(\dfrac{1}{\sqrt{3+x^2}+2}+\dfrac{2}{2x-1}\right)=0\)
TH1:\(x^2-1=0\Leftrightarrow\left[{}\begin{matrix}x=1\left(tm\right)\\x=-1\left(tm\right)\end{matrix}\right.\)
TH2:\(\dfrac{1}{\sqrt{3+x^2}+2}+\dfrac{2}{2x-1}=0\)
\(\Rightarrow2x-1+4+2\sqrt{3+x^2}=0\)
\(\Leftrightarrow2x+3+2\sqrt{3+x^2}=0\)
Ta có: \(2x+3+2\sqrt{3+x^2}\ge2x+3+2\sqrt{x^2}=2x+3+2\left|x\right|\ge2x+3-2x=3>0\)
nên trong TH2, pt vô nghiệm
Vậy pt đã cho có tập nghiệm \(S=\left\{-1;1\right\}\)