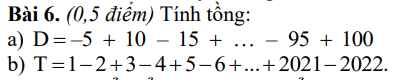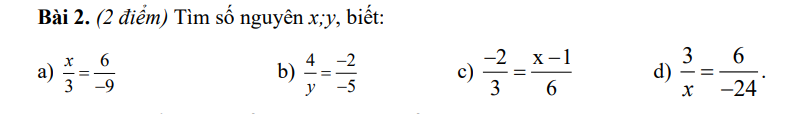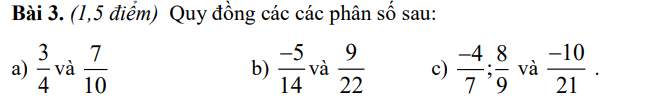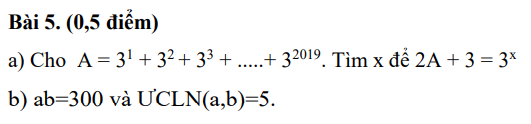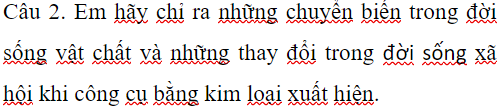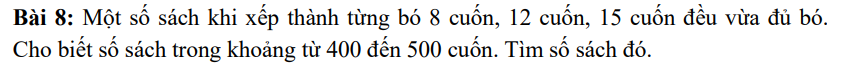Question

mn ơi làm hộ mình bài này với,ai làm nhanh nhất mình tim cho ! ​

Answer 1

2,

\(a,\dfrac{2}{1.3}+\dfrac{2}{3.5}+...+\dfrac{2}{97.99}\\ =1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+...+\dfrac{1}{97}-\dfrac{1}{99}\\ =1-\dfrac{1}{99}\\ =\dfrac{98}{99}\)

\(b,\dfrac{1}{1.4}+\dfrac{1}{4.7}+...+\dfrac{1}{40.43}\\ =\left(\dfrac{3}{1.4}+\dfrac{3}{4.7}+...+\dfrac{3}{40.43}\right):3\\ =\left(1-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{7}+...+\dfrac{1}{40}-\dfrac{1}{43}\right):3\\ =\left(1-\dfrac{1}{43}\right):3\\ =\dfrac{42}{43}:3=\dfrac{14}{43}\)

Answer 2

\(1,\dfrac{a}{n\left(n+a\right)}=\dfrac{\left(a+n\right)-n}{n\left(a+n\right)}=\dfrac{a+n}{n\left(a+n\right)}-\dfrac{n}{n\left(a+n\right)}=\dfrac{1}{n}-\dfrac{1}{a+n}\)