\(a.\) Xét \(\Delta AEM\) vuông tại E và \(\Delta AFM\) vuông tại F:
\(\widehat{EAM}=\widehat{FAM}\) \((\)AM là phân giác \(\widehat{BAC}\)\().\)
\(AM\) \(chung.\)
\(\Rightarrow\) \(\Delta AEM\) \(=\Delta AFM\left(ch-gn\right).\)
\(b.\) Xét \(\Delta BEM\) vuông tại E:
BE; EM là 2 cạnh góc vuông.
BM là cạnh huyền.
\(\Rightarrow\) \(BM>BE;ME.\)
Vì \(\Delta AEM\) \(=\Delta AFM\left(cmt\right).\)
\(\Rightarrow ME=MF\) (2 cạnh tương ứng).
Mà \(BM>ME.\)
\(\Rightarrow BM>MF.\)


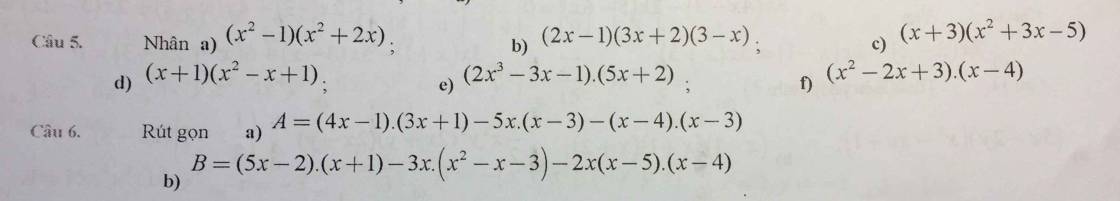
 giúp mk với mn mk đang gấp
giúp mk với mn mk đang gấp
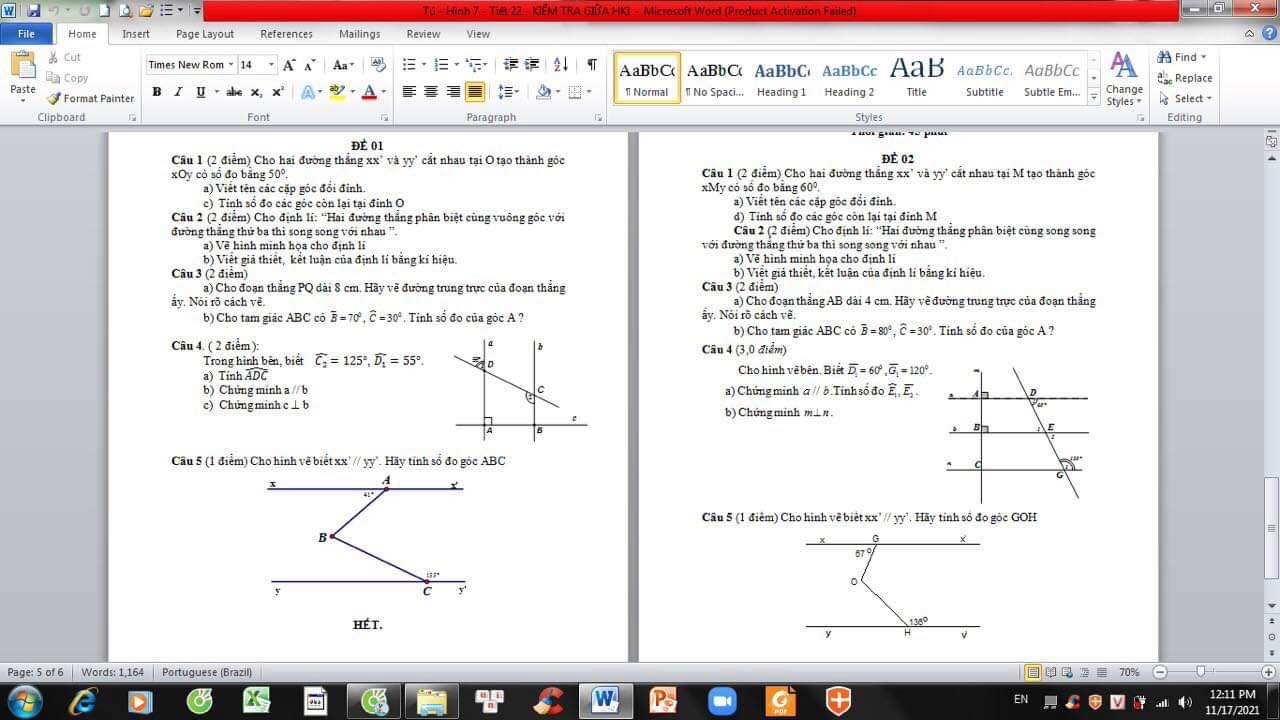
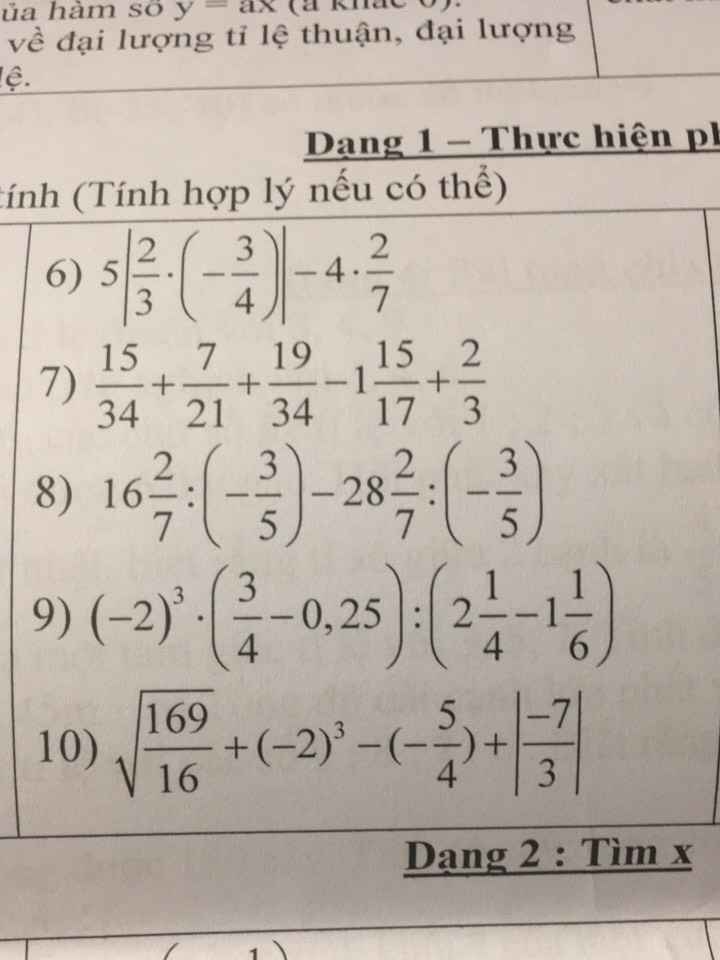
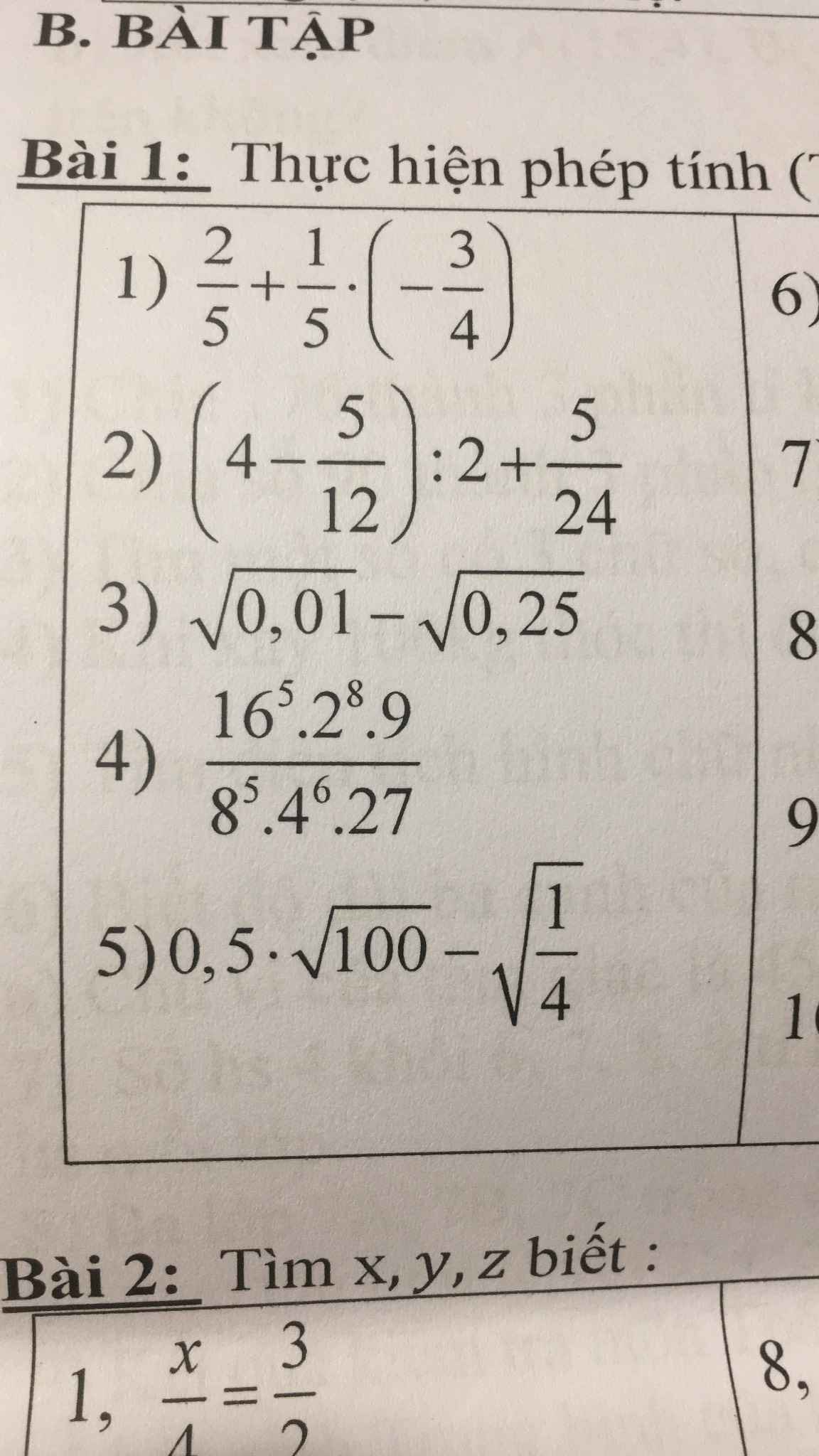
 giúp mình với, mk đang cần gấp ạ ! thanks mn rất nhiều ạ
giúp mình với, mk đang cần gấp ạ ! thanks mn rất nhiều ạ