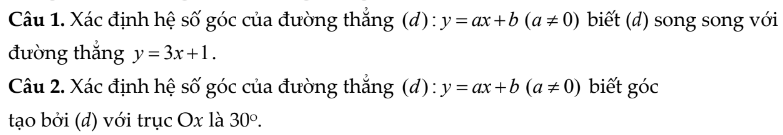\(a)A\ge\dfrac{x-\sqrt{x}-3}{\sqrt[]{x}}\Leftrightarrow\dfrac{\sqrt{x}-4}{\sqrt{x}}\ge\dfrac{x-\sqrt{x}-3}{\sqrt{x}}\)
\(\Leftrightarrow\sqrt{x}-4\ge x-\sqrt{x}-3\)
\(\Leftrightarrow x-2\sqrt{x}+1\le0\)
\(\Leftrightarrow(\sqrt{x}-1)^2\le0\)
\(\Leftrightarrow\sqrt{x}-1=0\Leftrightarrow\sqrt{x}=1\Leftrightarrow x=1\left(tm\right)\)
\(b)ĐKXĐ:x>0;x\ne4\)
\(B=\dfrac{x+2\sqrt{x}-10}{x-2\sqrt{x}}+\dfrac{\sqrt{x}-1}{\sqrt{x}-2}-\dfrac{\sqrt{x}+2}{\sqrt{x}}\)
\(=\dfrac{x+2\sqrt{x}-10}{\sqrt{x}\left(\sqrt{x}-2\right)}+\dfrac{\sqrt{x}(\sqrt{x}-1)}{\sqrt{x}\left(\sqrt{x}-2\right)}-\dfrac{(\sqrt{x}+2)(\sqrt{x}-2)}{\sqrt{x}\left(\sqrt{x}-2\right)}\)
\(=\dfrac{x+2\sqrt{x}-10+x-\sqrt{x}-x+4}{\sqrt{x}\left(\sqrt{x}-2\right)}\)
\(=\dfrac{x+\sqrt{x}-6}{\sqrt{x}\left(\sqrt{x}-2\right)}=\dfrac{(\sqrt{x}+3)\left(\sqrt{x}-2\right)}{\sqrt{x}\left(\sqrt{x}-2\right)}\)
\(=\dfrac{\sqrt{x}+3}{\sqrt{x}}\left(đpcm\right)\)
\(c)\dfrac{A}{B}=\dfrac{\sqrt{x}-4}{\sqrt{x}+3}\Rightarrow\left|\dfrac{A}{B}\right|=\dfrac{\left|\sqrt{x}-4\right|}{\sqrt{x}+3}\left(vì\sqrt{x}+3>0\right)\)
Xét các TH:
\(TH1:\sqrt{x}-4< 0\Leftrightarrow\sqrt{x}< 4\Leftrightarrow x< 16\left(1\right)\)
\(\Rightarrow\left|\dfrac{A}{B}\right|=\dfrac{4-\sqrt{x}}{\sqrt{x}+3}\)
\(\left|\dfrac{A}{B}\right|>\dfrac{A}{B}\Leftrightarrow\dfrac{4-\sqrt{x}}{\sqrt{x}+3}>\dfrac{\sqrt{x}-4}{\sqrt{x}+3}\)
\(\Leftrightarrow4-\sqrt{x}>\sqrt{x}-4\Leftrightarrow2\sqrt{x}< 8\Leftrightarrow\sqrt{x}< 4\)
\(\Leftrightarrow x< 16\left(2\right)\)
Từ (1)(2) suy ra x<16 suy ra x lớn nhất bằng 15
\(TH2:\sqrt{x}-4\ge0.\) Giai tương tự TH1 suy ra loại

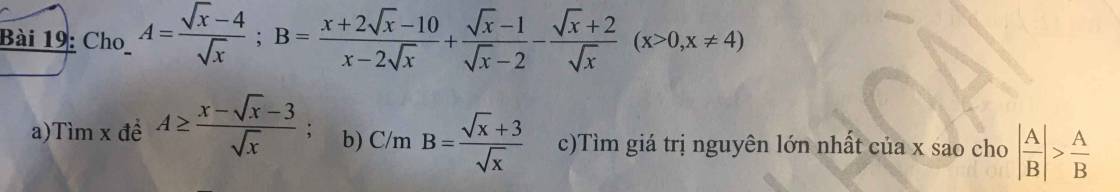


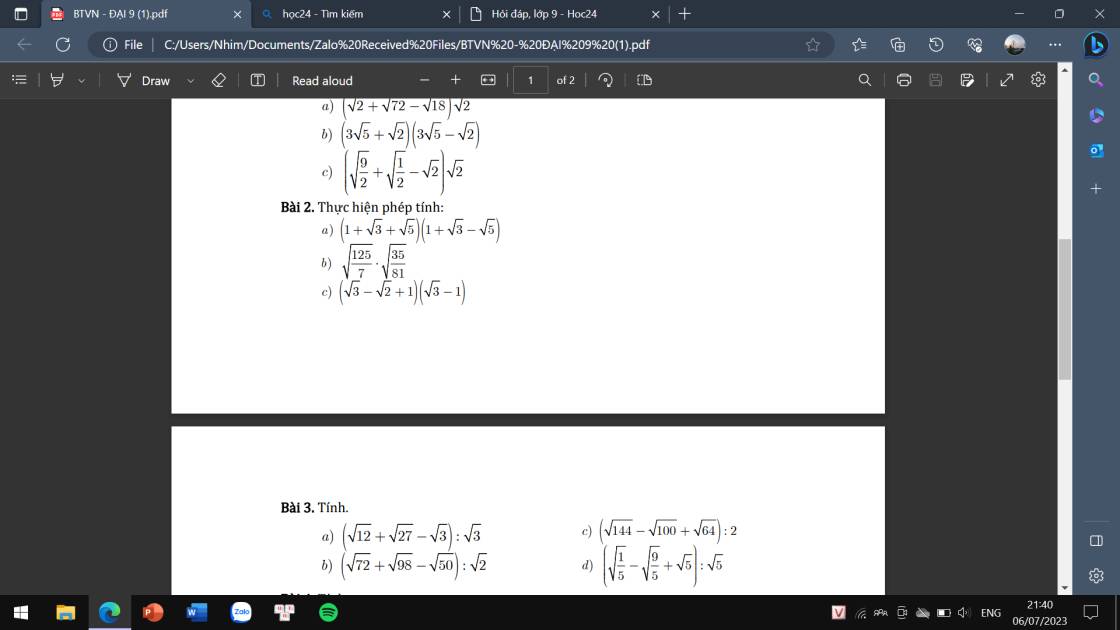
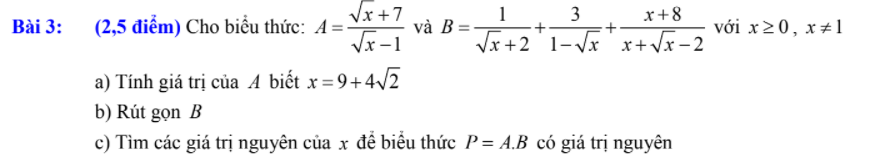 được không ạ, mai em phải nộp rồi, cảm ơn mn nhiều.
được không ạ, mai em phải nộp rồi, cảm ơn mn nhiều.  này được
này được 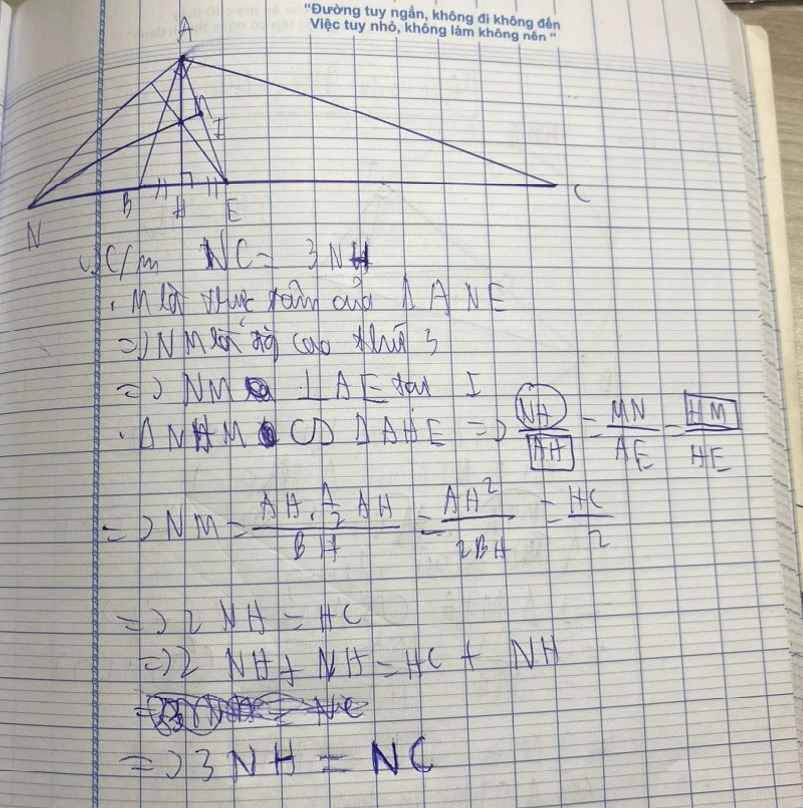 bạn nào có thể làm giúp mình bài này theo những ý như này được không ạ
bạn nào có thể làm giúp mình bài này theo những ý như này được không ạ