\(a,4x\left(x-1\right)-\left(x+3\right)\left(x-3\right)=9\\ \Leftrightarrow4x^2-4x-x^2+9-9=0\\ \Leftrightarrow3x^2-4x=0\\ \Leftrightarrow x\left(3x-4\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{4}{3}\end{matrix}\right.\)
b, ĐKXĐ:\(\left\{{}\begin{matrix}x\ne0\\x\ne2\end{matrix}\right.\)
\(\dfrac{x}{x-2}+\dfrac{1}{x}=1\\ \Leftrightarrow\dfrac{x^2}{x\left(x-2\right)}+\dfrac{x-2}{x\left(x-2\right)}=1\\ \Leftrightarrow\dfrac{x^2+x-2}{x^2-2x}=1\\ \Leftrightarrow x^2+x-2=x^2-2x\\ \Leftrightarrow3x=2\\ \Leftrightarrow x=\dfrac{2}{3}\left(tm\right)\)
a, 4x(x-1)-(x-3) (x+3)=9
<=> 4x2-4x - (x2-9) =9
<=> 4x2-4x-x2+9 =9
<=> 3x2-4x =0
<=> x(3x-4) =0
=> x= 0 hoặc 3x-4=0
=> x=0 hoặc x= 4/3




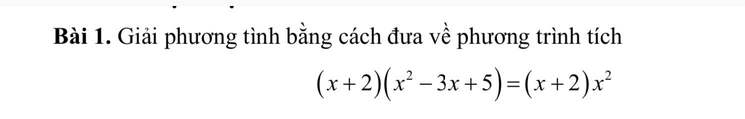

 vẽ hình giúp mik nha mik cảm ơn rất rất nhiều
vẽ hình giúp mik nha mik cảm ơn rất rất nhiều


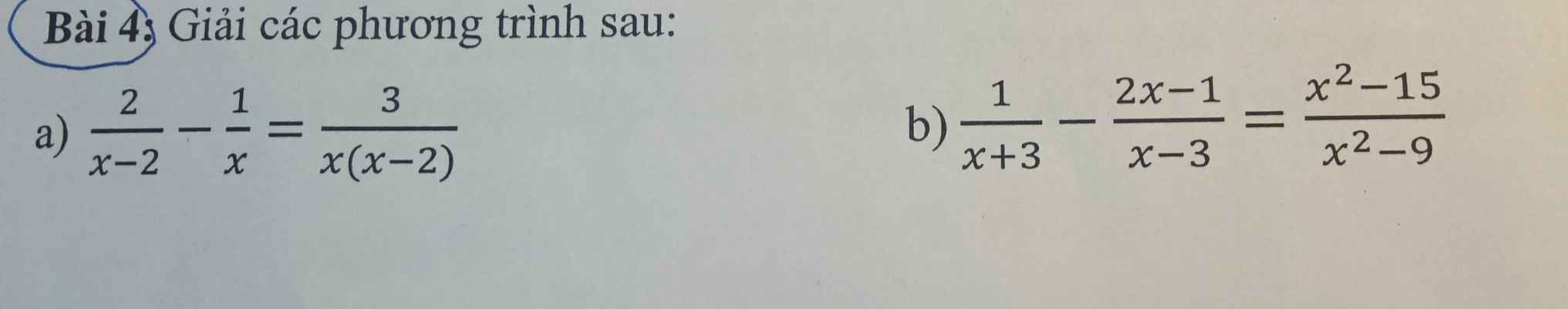
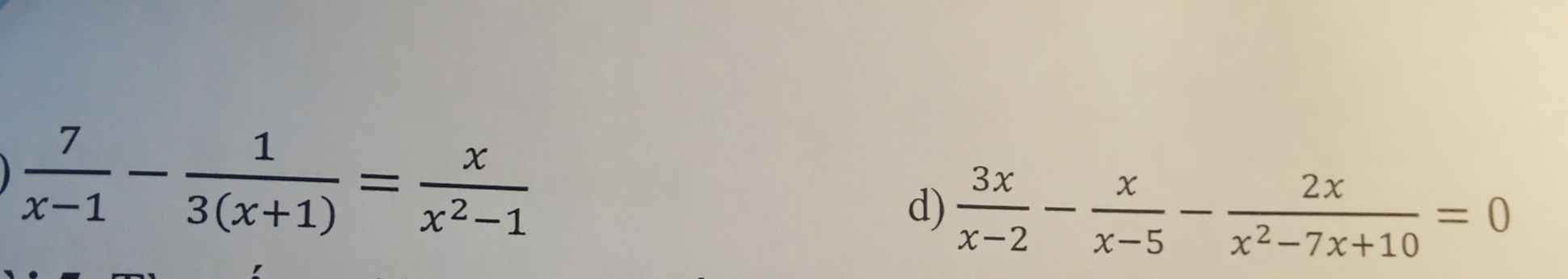 Mn giúp mik vs
Mn giúp mik vs