\(a,\dfrac{5\left(1-2x\right)}{3}+\dfrac{x}{2}=\dfrac{3\left(x-5\right)}{4}-2\\ \Leftrightarrow\dfrac{20\left(1-2x\right)}{12}+\dfrac{6x}{12}-\dfrac{9\left(x-5\right)}{12}+\dfrac{24}{12}=0\\ \Leftrightarrow20-40x+6x-9x+45+24=0\\ \Leftrightarrow-43x+89=0\\ \Leftrightarrow x=\dfrac{89}{43}\)
b, ĐKXĐ:\(x\ne\pm1\)
\(\dfrac{3}{x-1}=\dfrac{3x+2}{1-x^2}-\dfrac{4}{x+1}\\ \Leftrightarrow\dfrac{3\left(x+1\right)}{\left(x+1\right)\left(x-1\right)}+\dfrac{3x+2}{\left(x+1\right)\left(x-1\right)}+\dfrac{4\left(x-1\right)}{\left(x+1\right)\left(x-1\right)}=0\\ \Leftrightarrow\dfrac{3x+3+3x+2+4x-4}{\left(x+1\right)\left(x-1\right)}=0\\ \Rightarrow10x+1=0\\ \Leftrightarrow x=-\dfrac{1}{10}\left(tm\right)\)




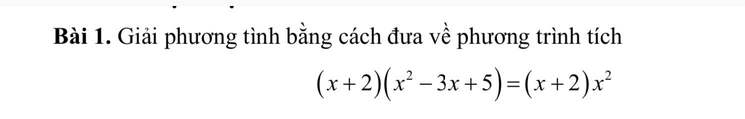

 vẽ hình giúp mik nha mik cảm ơn rất rất nhiều
vẽ hình giúp mik nha mik cảm ơn rất rất nhiều


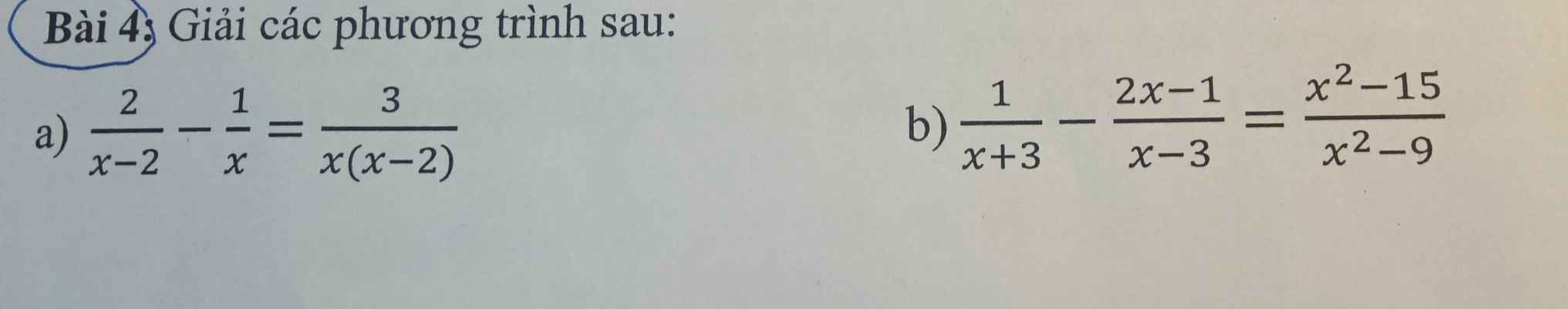
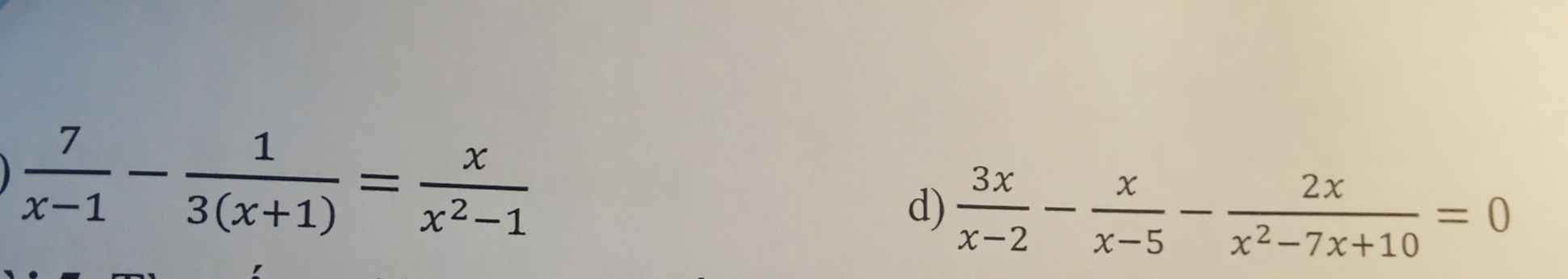 Mn giúp mik vs
Mn giúp mik vs