ĐK \(x\ge-1\)
\(5\sqrt{x^3+1}=2\left(x^2+2\right)< =>5\sqrt{\left(x+1\right)\left(x^2-x+1\right)}=2\left(x^2+2\right)\)
Đặt \(\sqrt{\left(x+1\right)}=a.\sqrt{\left(x^2-x+1\right)}=b\left(a,b\ge0\right)\)
\(=>a^2+b^2=x+1+x^2=x+1=x^2+2\)
Thay vào ta đc
\(5ab=2\left(a^2+b^2\right)=>-2a^2-2b^2+5ab=0=>\left(2a-b\right)\left(2b-a\right)=0\)
Ta có \(2b-a=0=>2a=b=>2\sqrt{x+1}=\sqrt{x^2-x+1}\)
\(=>4x+4=x^2-x+1=>x^2-5x-3=0\)
\(\Delta=37>0\) (pt có 2 nghiệm phân biệt)
\(x_1=\dfrac{5+\sqrt{37}}{2}\) (nhận) \(x_2=\dfrac{5-\sqrt{37}}{2}\) nhận
=> PT ban đầu có 2 nghiệm \(x_1=\dfrac{5+\sqrt{37}}{2}\) và \(x_2=\dfrac{5-\sqrt{37}}{2}\)
Đúng 1
Bình luận (0)
Các câu hỏi tương tự
Cho 3 số a,b,c dương thỏa mãn (a+b)(a+c)=8.
Tìm GTLN của biểu thức A=abc(a+b+c)
MN giúp em bài này vs ak. rồi em tick luôn cho ak...em đang cần gấp, mong mn giúp ạ!
Giúp mik bài này vs ạ mik đang cần gấp
Mong mn giúp em giải pt này vs ạ! Em đg cần gấp lắm ạ ! Em cảm ơn
Giúp em bài này với mn ơi em đang cần gấp
Mọi người ơi, giúp em bài này vớ ạ, em đang cần gấp lắm ạ, cảm ơn mng rất rất nhiều ạ.
Coá ai ko giúp em bài này với ạ. Em đang cần gấp trước 1h00 . Em xin cảm ơn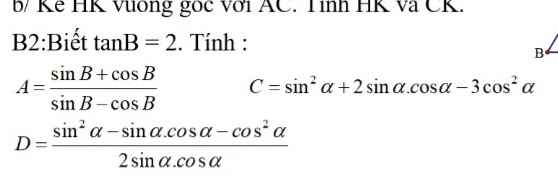
mn giúp em vs ạ. bài này em khó hiểu quá ạ
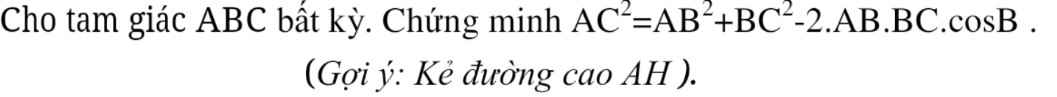

MỌI NGƯỜI GIÚP EM CÂU C VS Ạ EM ĐANG CẦN GẤP CẢM ƠN MN Ạ
Tính:a.sqrt{4+sqrt{7}} - sqrt{4-sqrt{7}}b.sqrt{4-sqrt{15}} - sqrt{4+sqrt{15}}c.sqrt{2+sqrt{3}} + sqrt{2-sqrt{3}}d.sqrt{9+sqrt{17}} - sqrt{9-sqrt{17}}Mong mn giúp em bài này ạ .Em đang cần gấp !!
Đọc tiếp
Tính:
a.\(\sqrt{4+\sqrt{7}}\) - \(\sqrt{4-\sqrt{7}}\)
b.\(\sqrt{4-\sqrt{15}}\) - \(\sqrt{4+\sqrt{15}}\)
c.\(\sqrt{2+\sqrt{3}}\) + \(\sqrt{2-\sqrt{3}}\)
d.\(\sqrt{9+\sqrt{17}}\) - \(\sqrt{9-\sqrt{17}}\)
Mong mn giúp em bài này ạ .Em đang cần gấp !!
giúp em với ạ em đang cần gấp mn giúp em 


