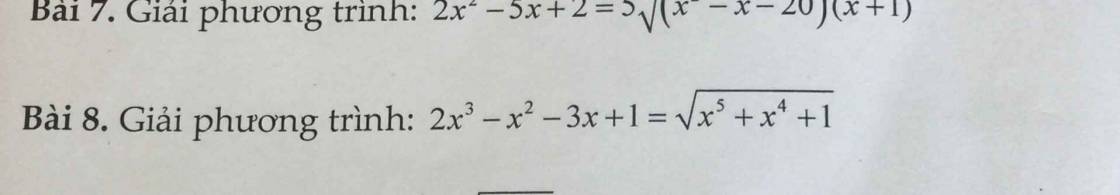\(x^5+x^4+1=\left(x^2+ax+1\right)\left(x^3+bx^2+cx+1\right)\)
\(a=1;b=0;c=-1\)
\(=>2\left(x^2-x+1\right)-\left(x^2+x+1\right)-\sqrt{\left(x^2-x+1\right)-\left(x^2+x+1\right)}=0\)
\(2.\left(\dfrac{x^3-x+1}{x^2+x+1}\right)-\sqrt{\left(\dfrac{x^3-x+1}{x^2+x+1}\right)}-1=0\)
Đặt \(1=\sqrt{\left(\dfrac{x^3-x+1}{x^2+x+1}\right)}>0\) ta đc
PT \(2t^2-t-1=0< =>\left[{}\begin{matrix}t=1\\t=\dfrac{-1}{2}\end{matrix}\right.\)
\(t=1< =>\dfrac{x^3-x+1}{x^2+x+1}=1< =>x^3-x^2-2x=0< =>\left[{}\begin{matrix}x=0\\x=-1\\x=2\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Các câu hỏi tương tự
Cho 3 số a,b,c dương thỏa mãn (a+b)(a+c)=8.
Tìm GTLN của biểu thức A=abc(a+b+c)
MN giúp em bài này vs ak. rồi em tick luôn cho ak...em đang cần gấp, mong mn giúp ạ!

MỌI NGƯỜI GIÚP EM CÂU C VS Ạ EM ĐANG CẦN GẤP CẢM ƠN MN Ạ
giúp em với ạ em đang cần gấp mn giúp em 
 Em cần giúp câu c và d ạ, mn giúp em với em đang cần gấp
Em cần giúp câu c và d ạ, mn giúp em với em đang cần gấp
Mn giúp em với ạ em đang cần gấp
giúp mik vs, mik đang cần gấp (bài b5 nha mn)
Giúp vs ạ em đang cần gấp hôm nay ạ
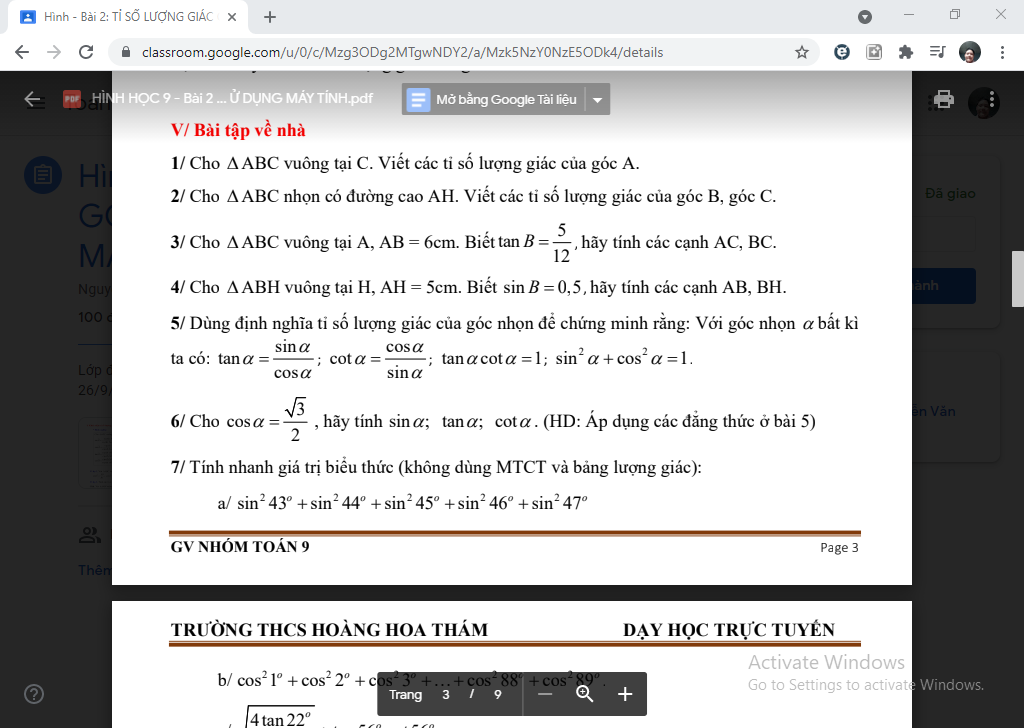
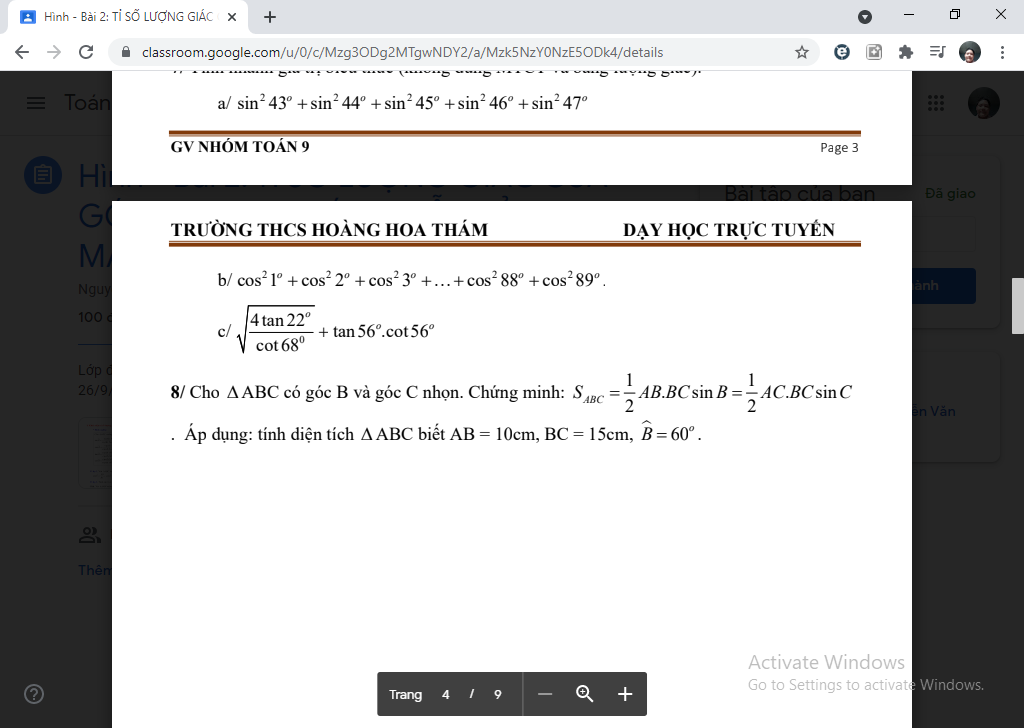
giải giúp em vs ạ em đang cần gấp.
Mn lm giúp mik bài 9 vs ạ . Lm ơn mik đang rất cần
Giúp em với mn ơi đang cần gấp ạ !!!!!