Với m = 3 thì (d): y = 8x - 7
PTHĐGĐ của (P) và (d): \(x^2-8x+7=0\)
Có: \(a+b+c=1+\left(-8\right)+7=0\)
=> PT có 2 nghiệm phân biệt \(x_1=1;x_2=7\)
\(x_1=1\Rightarrow y_1=x_1^2=1^2=1\\ x_2=7\Rightarrow y_2=x_2^2=7^2=49\)
Tọa độ giao điểm của (P) và (d) là: \(\left(1;1\right);\left(7;49\right)\)
b)
PTHĐGĐ của (P) và (d) là:
\(x^2-2\left(m+1\right)x+3m-2=0\)
\(\Delta'=\left(m+1\right)^2-\left(3m-2\right)=m^2+2m+1-3m+2=m^2-m+3\\ =m^2-m+\dfrac{1}{4}+\dfrac{11}{4}=\left(m-\dfrac{1}{2}\right)^2+\dfrac{11}{4}>0\forall m\)
Theo vi ét: \(\left\{{}\begin{matrix}x_1+x_2=2m+2\\x_1x_2=3m-2\end{matrix}\right.\)
Theo đề: \(x_1^2+x_2^2=20\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=20\\ \Leftrightarrow\left(2m+2\right)^2-2\left(3m-2\right)=20\)
\(\Leftrightarrow4m^2+8m+4-6m+4=20\\ \Leftrightarrow4m^2+2m+8-20=0\\ \Leftrightarrow4m^2+2m-12=0\\ \Leftrightarrow2m^2+m-6=0\)
\(\Rightarrow\left\{{}\begin{matrix}m=-2\left(tm\right)\\m=\dfrac{3}{2}\left(tm\right)\end{matrix}\right.\)
Gọi tọa độ của \(\left(P\right),\left(d\right)\) là \(A\left(x_A;y_A\right),B\left(x_B;y_B\right)\)
\(a,m=3\)
\(\Rightarrow x^2=2\left(3+1\right)x-3.3+2\)
\(\Rightarrow x^2-8x+7=0\)
\(\Rightarrow\left\{{}\begin{matrix}x=7\\x=1\end{matrix}\right.\)
Thay \(x=7\) vào \(\left(P\right):y=x^2\Rightarrow y=7^2=49\)
Khi m = 3 thì đường thẳng \(\left(d\right):y=2\left(3+1\right)x-3.3+2=8x-7\)
Thay \(x=1\) vào \(\left(d\right):y=8x-7=8.1-7=1\)
Vậy \(A\left(7;49\right),B\left(1;1\right)\)
\(\Rightarrow y=\left(2m+2\right)x-3m+2\)
\(b,\) Vì \(\left(P\right)\) và \(\left(d\right)\) luôn cắt nhau tại 2 điểm pb A,B \(\forall m\) nên :
\(x^2=2\left(m+1\right)x-3m+2\Leftrightarrow x^2-2\left(m+1\right)x+3m-2\)
Theo Vi-ét, ta có : \(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=2m+2\\x_1x_2=\dfrac{c}{a}=3m-2\end{matrix}\right.\)
Ta có : \(x_1^2+x_2^2=20\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2\)
\(\Leftrightarrow\left(2m+2\right)^2-2\left(3m-2\right)=20\)
\(\Leftrightarrow4m^2+8m+4-6m+4-20=0\)
\(\Leftrightarrow4m^2+2m-12=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}m=\dfrac{3}{2}\\m=-2\end{matrix}\right.\)
Vậy \(m=\dfrac{3}{2},m=-2\) thì thỏa mãn đề bài.





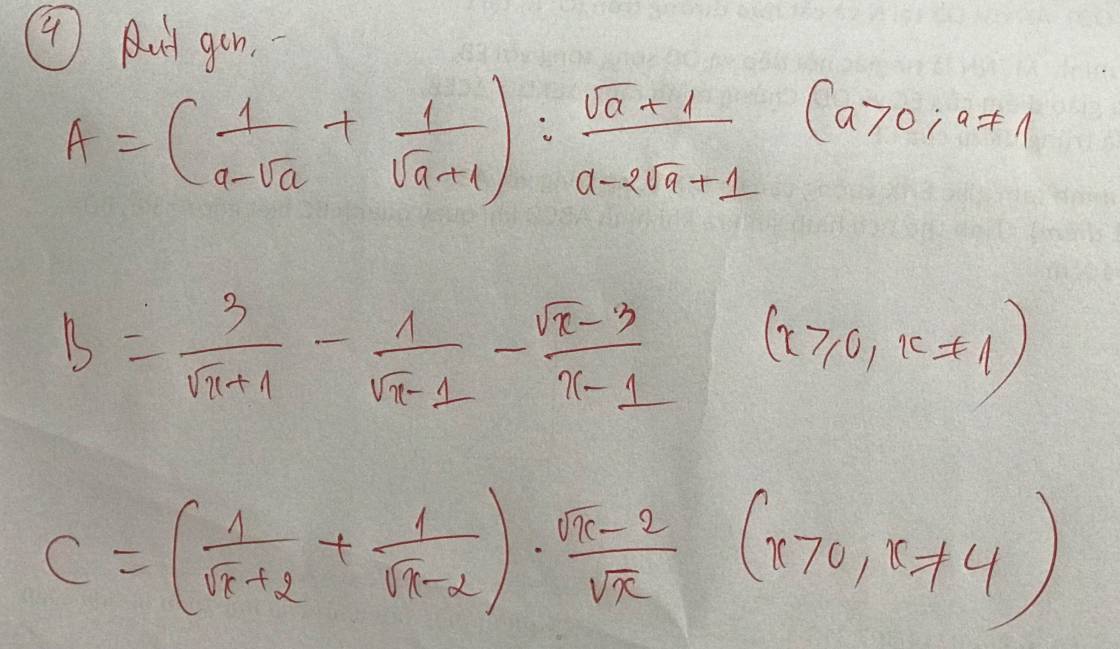



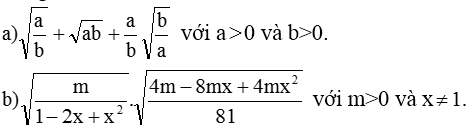
 Giúp mình bài này với ạ, mình cần lời giải chi tiết. Mình cảm ơn
Giúp mình bài này với ạ, mình cần lời giải chi tiết. Mình cảm ơn