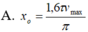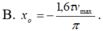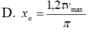Đáp án D
M cđ tròn đều trên (C), còn P dao động điều hòa trên d.
Khi P và M gặp nhau thì P sẽ ở biên của dao động, khoảng thời gian giữa 2 lần liên tiếp P và M gặp nhau chính là τ = T 2
Tốc độ của P: v P = A ω c os ( ω t + φ ) , trong đó A = d / 2 .
Tốc độ của M: v M = ω r ; lại thấy r = d / 2 = A nên v M = A ω
Như vậy, v P = 1 2 v M ⇔ v P = ± v P max 2 ⇔ x P = ± A 3 2 (1)
Dễ thấy, khi đi từ biên về, cần 1 thời gian nhỏ nhất là Δ t = T 12 để (1) xảy ra.
⇒ Δ t = τ 6