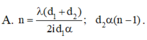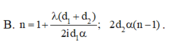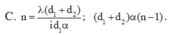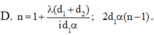Lưỡng lăng kính được ghép từ hai lăng kính giống hệt nhau, có góc chiết quang nhỏ A1 = A2 = A, chiết suất n1 = n2 = n. Nguồn sáng đơn sắc S đặt trên trục đối xứng, cách lưỡng lăng kính một đoạn d, màn ảnh cách lưỡng lăng kính một đoạn l. Cho rằng do A bé nên tanA = A, và bỏ qua chiều dày của đáy lăng kính. Tìm số vân sáng trên màn, với d = 0,5m; l = 1,5m; A = 4.10-3rad; n = 1,5; l = 0,6mm.
A. 15 vân sáng
B. 13 vân sáng
C. 11 vân sáng
D. 14 vân sáng
Đáp án: C
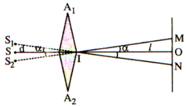
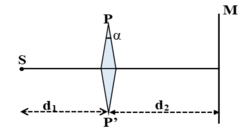
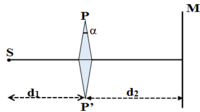
Do lăng kính có góc A bé, hai ảnh được tạo thành và S nằm trên cùng một đường thẳng, khoảng cách vật - ảnh là: (Hình vẽ)
SS1 = SS2 = dtana = dtanA(n - 1)
a = S1S2 = 2dtanA(n - 1), với A bé
Þ a = 2dA(n - 1) (1)
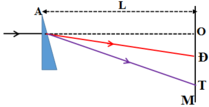
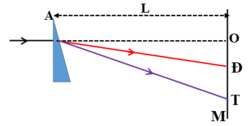
Trường giao thoa là vùng MN, trong đó các góc:
![]()
Bề rộng của vùng giao thoa: OM = ON = ltana = ltanA(n - 1)
Do góc bé, nên MN = 2lA(n - 1) (2)
Từ (1), ta có: a = 2.0,5.4.10-3.(1,5 - 1) = 2.10-3m
D = l + d = 2m
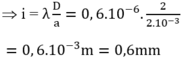
Tọa độ vân sáng: x = ki, (với - ON £ ki £ OM).
Với OM = ON = lA(n - 1) = 1,5.4.10-3.(1,5 - 1) = 3.10-3m.
Ta có: OM/i = 5. Vậy có 11 vân sáng.