\(\left\{{}\begin{matrix}\widehat{AOD}+\widehat{BOC}=180^0\\\widehat{AOD}=\widehat{BOC}\left(đối.đỉnh\right)\end{matrix}\right.\Rightarrow\widehat{AOD}=\widehat{BOC}=90^0\\ \Rightarrow AB\perp CD\\ \Rightarrow\widehat{AOD}=\widehat{BOD}=\widehat{BOC}=\widehat{AOC}=90^0\)
Ta có: \(\widehat{AOD}=\widehat{BOC}\)(đối đỉnh)
Mà \(\widehat{AOD}+\widehat{BOC}=100^0\)
\(\Rightarrow\widehat{AOD}=\widehat{BOC}=50^0\)
Ta có: \(\widehat{AOD}+\widehat{AOC}=180^0\)(kề bù)
\(\Rightarrow\widehat{AOC}=180^0-\widehat{AOD}=130^0\)
\(\Rightarrow\widehat{DOB}=\widehat{AOC}=130^0\)(đối đỉnh)




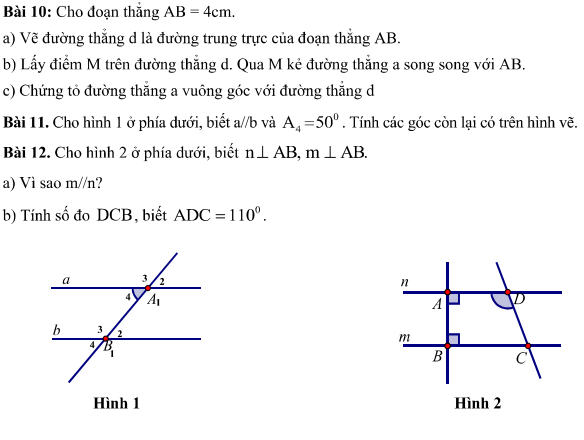


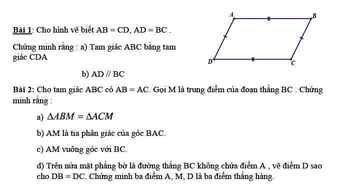
 mọi nguời giúp em gấp với ạ,chiều em phải nộp rồi,không cần hình đâu ạ!em cảm ơn !
mọi nguời giúp em gấp với ạ,chiều em phải nộp rồi,không cần hình đâu ạ!em cảm ơn ! giúp em với ạ e, đang cần gấp lắm ạ
giúp em với ạ e, đang cần gấp lắm ạ