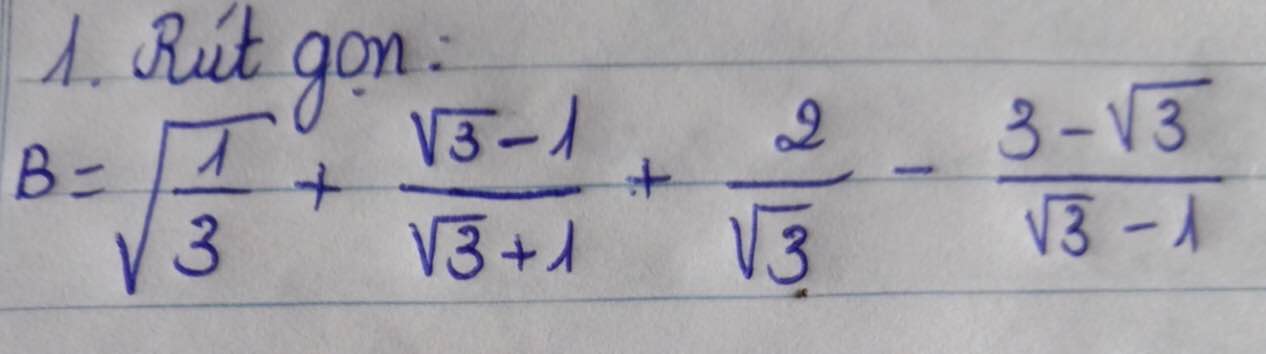\(B=\sqrt{\dfrac{1}{3}}+\dfrac{\sqrt{3}-1}{\sqrt{3}+1}+\dfrac{2}{\sqrt{3}}-\dfrac{3-\sqrt{3}}{\sqrt{3}-1}\)
\(\Rightarrow B=\dfrac{\sqrt{1}}{\sqrt{3}}+\dfrac{\left(\sqrt{3}-1\right)^2}{\left(\sqrt{3}+1\right)\left(\sqrt{3}-1\right)}+\dfrac{2}{\sqrt{3}}-\dfrac{\sqrt{3}\left(\sqrt{3}-1\right)}{\sqrt{3}-1}\)
\(\Rightarrow B=\left(\dfrac{1}{\sqrt{3}}+\dfrac{2}{\sqrt{3}}\right)+\dfrac{3-2\sqrt{3}+1}{\left(\sqrt{3}+1\right)\left(\sqrt{3}-1\right)}-\sqrt{3}\)
\(\Rightarrow B=\dfrac{3}{\sqrt{3}}+\dfrac{4-2\sqrt{3}}{\left(\sqrt{3}+1\right)\left(\sqrt{3}-1\right)}-\sqrt{3}\)
\(\Rightarrow B=\sqrt{3}+\dfrac{4-2\sqrt{3}}{\sqrt{3^2}-1^2}-\sqrt{3}\)
\(\Rightarrow B=\dfrac{4-2\sqrt{3}}{2}\)
\(\Rightarrow B=2-\sqrt{3}\)
⇔ \(B=\dfrac{1}{\sqrt{3}}+\dfrac{\left(\sqrt{3}-1\right)\left(\sqrt{3}-1\right)}{\left(\sqrt{3}-1\right)\left(\sqrt{3}+1\right)}+\dfrac{2}{\sqrt{3}}-\dfrac{\sqrt{3}\left(\sqrt{3}-1\right)}{\sqrt{3}-1}\)
⇔ \(B=\dfrac{\text{3}}{\sqrt{3}}+\dfrac{3-2\sqrt{3}+1}{3-1}-\sqrt{3}\)
⇔ \(B=\sqrt{3}+\dfrac{\text{4}-2\sqrt{3}}{\text{2}}-\sqrt{3}\)
⇔ \(B=\dfrac{2\left(2-\sqrt{3}\right)}{2}=2-\sqrt{3}\)