Chọn đáp án B.
Theo lý thuyết cơ bản về các khối đa diện đều ta có đáp án là B.
Chọn đáp án B.
Theo lý thuyết cơ bản về các khối đa diện đều ta có đáp án là B.
Khối hai mươi mặt đều thuộc khối đa diện loại nào?
A. loại 3 ; 5
B. loại 5 ; 3
C. loại 3 ; 4
D. loại 4 ; 3
Cho khối lập phương ABCD.A’B’C’D’. Cắt khối lập phương bởi các mặt phẳng (AB’D’) và (C’BD) ta được ba khối đa diện. Xét các mệnh đề sau:
(I): Ba khối đa diện thu được gồm hai khối chóp tam giác đều và một khối lăng trụ tam giác.
(II): Ba khối đa diện thu được gồm hai khối tứ diện và một khối bát diện đều.
(III): Trong ba khối đa diện thu được có hai khối đa diện bằng nhau.
Số mệnh đề đúng là
A. 3
B. 2
C. 0
D. 1
Cho khối lập phương ABCD.A’B’C’D’. Cắt khối lập phương trên bởi các mặt phẳng (AB’D’) và (C’BD) ta được ba khối đa diện. Xét các mệnh đề sau:
(I): Ba khối đa diện thu được gồm hai khối chóp tam giác đều và một khối lăng trụ tam giác.
(II): Ba khối đa diện thu được gồm hai khối tứ diện và một khối bát diện đều
(III): Trong ba khối đa diện thu được có hai khối đa diện bằng nhau
Số mệnh đề đúng là:
A. 2
B. 1
C. 3
D. 0
Khối đa diện mười hai mặt đều là khối đa diện đều loại:
A. {3;3}
B. {5;3}
C. {3;5}
D. {4;3}
Tính tổng diện tích tất cả các mặt của khối đa diện đều loại {3;5} có cạnh bằng 1.
A. 5 3 2
B. 5 3
C. 3 3
D. − 3 3 2
Tính tổng diện tích tất cả các mặt của khối đa diện đều loại {3;5} có cạnh bằng 1
A. 5 3 2
B. 5 3
C. 3 3
D. 3 3 2
Cho các khối đa diện đều như hình vẽ sau đây. Khối đa diện đều loại {3;5} là hình nào?
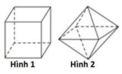
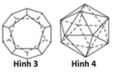
A. Hình 4
B. Hình 1
C. Hình 2
D. Hình 3
Hai khối đa diện đều được gọi là đối ngẫu nếu các đỉnh của khối đa diện đều loại này là tâm (đường tròn ngoại tiếp) các mặt của khối đa diện đều loại kia. Hãy tìm khẳng định sai trong các khẳng định sau:
A. Khối tứ diện đều đối ngẫu với chính nó.
B. Hai khối đa diện đều đối ngẫu với nhau luôn có số cạnh bằng nhau.
C. Số mặt của một đa diện đều bằng số cạnh của đa diện đều đối ngẫu với nó.
D. Khối 20 mặt đều đối ngẫu với khối 12 mặt đều.
Người ta gọt một khối lập phương bằng gỗ để lấy khối tám mặt đều nội tiếp nó (tức là khối có các đỉnh là các tâm của các mặt khối lập phương). Biết cạnh của khối lập phương bằng a . Thể tích khối tám mặt đều đó bằng
A. a 3 6
B. a 3 12
C. a 3 4
D. a 3 8
Cho khối chóp tứ giác đều S.ABCD. Gọi M là trung điểm SC, mặt phẳng (P) chứa AM và song song với BD chia khối lập phương thành hai khối đa diện, đặt V 1 là thể tích khối đa diện có chứa đỉnh S và V 2 là thể tích khối đa diện có chứa đáy ABCD. Tính V 1 V 2
A. V 1 V 2 = 1 3
B. V 1 V 2 = 1 2
C. V 1 V 2 = 2
D. V 1 V 2 = 3 2