Đáp án là D.
S Δ S B C = 1 2 S B . B C = 1 2 2 a . a = a 2 .
Gọi h = d A ; S B C ⇒ h = 3 V S . A B C S S B C = 3 a 3 a 2 = 3 a .
Đáp án là D.
S Δ S B C = 1 2 S B . B C = 1 2 2 a . a = a 2 .
Gọi h = d A ; S B C ⇒ h = 3 V S . A B C S S B C = 3 a 3 a 2 = 3 a .
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, SA vuông góc với đáy, khoảng cách từ A đến mặt phẳng (SBC) bằng 3. Gọi α là góc giữa hai mặt phẳng (SBC) và (ABC), tính cos α khi thể tích khối chóp S . A B C nhỏ nhất.
A. cos α = 2 2
B. cos α = 1 3
C. cos α = 3 3
D. cos α = 2 3
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A. Biết SA vuông góc với mặt phẳng đáy và SB= a 10 ;BC=2a;SC=2a 3 Thể tích khối chóp S.ABC là:
A. 3 a 3 2
B. 3 a 3 2
C. 3 a 3
D. a 3
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, A B = A , B C = A 3. Biết rằng SA vuông góc với mặt phẳng đáy và diện tích xung quanh của khối chóp S.ABC bằng 5 a 2 3 2 . Tính theo a khoảng cách d từ A đến mặt phẳng (SBC) gần với giá trị nào nhất sau đây ?
A. 0,72 a
B. 0,90a
C. 0,80a
D. 1,12a
Cho hình chóp S.ABC có cạnh SA vuông góc với mặt đáy (ABC), tam giác ABC là tam giác cân tại A, AB = a, B A C ^ = 120 0 . Tính theo a khoảng cách từ A đến mặt phẳng (SBC), biết khối chóp S.ABC có thể tích bằng 3 a 3 24
A. a 2 4
B. a 6 4
C. 3 a 2 10
D. a 2
Cho khối chóp S.ABC có SA vuông góc với (ABC), đáy ABC là tam giác vuông cân tại A, BC = 2a. Góc giữa SB và (ABC) là 300. Tính thể tích khối chóp S.ABC
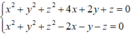
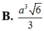
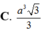
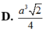
Cho hình chóp .S ABC có đáy ABC là tam giác vuông cân tại B, SA vuông góc với mặt đáy ( A B C ) , B C = a , góc hợp bởi (SBC) và SBC) là 60 0 Mặt phẳng (P) qua A vuông góc với SC cắt SB, SC lần lượt tại D, E. Thể tích khối đa diện ABCED là
A. a 3 3 6
B. 11 a 3 3 120
C. 11 a 3 3 60
D. 3 a 3 3 40
Cho khôi chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với đáy và khoảng cách từ điểm A đến mặt phẳng (SBC) bằng a 2 2 . Thể tích của khối chóp S.ABCD là
A. a 3 2
B. a 3
C. a 3 3 9
D. a 3 3
Cho hình chóp S.ABC có đáy là tam giác cân, AB=2a, B A C ^ = 120 ∘ ,SA=SB và mặt phẳng (SAB) vuông góc với mặt phẳng đáy, thể tích khối chóp đã cho bằng a 3 4 . Khoảng cách từ điểm A đến mặt phẳng (SBC) bằng
A. 21 a 7
B. 21 a 14
C. 15 a 10
D. 15 a 5
Cho hình chóp S.ABC có đáy là tam giác ABC vuông cân ở B, A C = a 2 . SA vuông góc với mặt phẳng (ABC) và (SA)=a. Gọi G là trọng tâm của tam giác SBC. Một mặt phẳng đi qua hai điểm A, G và song song với BC cắt SB, SC lần lượt tại B’ và C’. Thể tích khối chóp S.A’B’C’ bằng:
A. 2 a 3 9
B. 2 a 3 27
C. a 3 9
D. 4 a 3 27