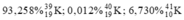Question

Kali có ba loại đồng vị là 39K (93,258%), 40K (0,012%) và 41K (6,73%)
a) Tính nguyên tử khối trung bình của Kali
b) Một quả chuối nặng 150g chứa 420mg kali. Tính khối lượng mỗi loại đồng vị trong quả chuối này.

Answer 1

a) \(\overline{A}=\dfrac{39.93,258+40.0,012+41.6,73}{100}=39,13472\)

b)

\(n_K=\dfrac{0,42}{39,13472}\approx0,0107\left(mol\right)\)

\(\left\{{}\begin{matrix}n_{^{39}K}=\dfrac{0,0107.93,258}{100}=0,01\left(mol\right)\\n_{^{40}K}=\dfrac{0,0107.0,012}{100}=1,3.10^{-6}\left(mol\right)\\n_{^{41}K}=\dfrac{0,0107.6,73}{100}=7,2.10^{-4}\left(mol\right)\end{matrix}\right.\)

=> \(\left\{{}\begin{matrix}m_{^{39}K}=0,01.39=0,39\left(g\right)\\m_{^{40}K}=1,3.10^{-6}.40=0,000052\left(g\right)\\m_{^{41}K}=7,2.10^{-4}.41=0,02952\left(g\right)\end{matrix}\right.\)