Đáp án B
Điều kiện x 2 − 1 ≥ 0 ⇒ x ≤ − 1 x ≥ 1 .
Phương trình đã cho tương đương với:
2 x 2 − 1 log 2 x 2 + 1 − 2 m 2 x 2 − 1 . log x 2 + 1 + 2 m + 8 = 0
⇔ 2 x 2 − 1 . log x 2 + 1 2 − 2 m 2 x 2 − 1 . log x 2 + 1 + 2 m + 8 = 0 *
Đặt t = x 2 ≥ 1 , theo bài ra ta có
1 ≤ x 1 < x 2 ≤ 3 ⇔ 1 ≤ x 1 2 < x 2 2 ≤ 9 ⇒ t ∈ 1 ; 9 .
Xét hàm số f t = 2 − t − 1 . log t + 1 trên đoạn 1 ; 9 .
Ta có f ' t = log t + 1 2 t − 1 + 2 t − 1 t + 1 . ln 10 > 0, ∀ ∈ 0 ; 9 ⇒ Hàm số f t đồng biến trên đoạn 1 ; 9 . Khi đó f 1 ≤ f t ≤ 9 hay 0 ≤ f t ≤ 4 .
Đặt u = 2 x 2 − 1 . log x 2 + 1 ⇒ u ∈ 0 ; 4 . Khi đó phương trình (*) trở thành u 2 − 2 m . u + 2 m + 8 = 0 1 .
Nhận thấy u=1 không phải là nghiệm của phương trình (1). Với u ≠ 1 thì phương trình (1) tương đương với
u 2 + 8 = 2 m u − 1 ⇔ 2 m = u 2 + 8 u − 1 2
Xét hàm số g u = u 2 + 8 u − 1 trên đoạn 0 ; 4 \ 1 .
Ta có g ' u = u 2 − 2 u − 8 u − 1 2 ; g ' u = 0 ⇔ u = 4 u = − 2 . Mà u ∈ 0 ; 4 \ 1 nên u=4.
Mặt khác, có g 0 = − 8 ; g 4 = 8 ; lim x → 1 − g u = − ∞ ; lim x → 1 + g u = + ∞ .
Bảng biến thiên:
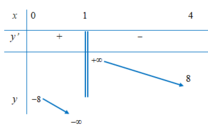
Yêu cầu bài toán <=>Phương trình (2) có nghiệm duy nhất trên đoạn 0 ; 4 \ 1 . Suy ra 2 m ≥ 8 2 m ≤ − 8 ⇔ m ≥ 4 m ≤ − 4 .
Mặt khác
m
∈
ℤ
,
m
∈
−
2017
;
2017
nên suy ra
4
≤
m
≤
2017
−
2017
≤
m
≤
−
4
.
Vậy có tất cả 2017 − 4 + 1 + − 4 + 2017 + 1 = 4028 giá trị m nguyên thỏa mãn bài toán.

