Các câu hỏi tương tự
Tìm họ nguyên hàm của hàm số lượng giác sau :
\(f\left(x\right)=\int\frac{4\sin x+3\cos x}{\sin x+2\cos x}dx\)
Cho hàm số
y
f
(
x
)
a
x
3
+
b
x
2
+
c
x
+
d
(a,b,cÎR, a≠0) có đồ thị (C). Biết đồ thị (C) đi qua A(1;4) và đồ thị hàm số
y
f
’
(
x
)
cho bởi hình vẽ. Giá trị
f
(
3
)
-
2...
Đọc tiếp
Cho hàm số y = f ( x ) = a x 3 + b x 2 + c x + d (a,b,cÎR, a≠0) có đồ thị (C). Biết đồ thị (C) đi qua A(1;4) và đồ thị hàm số y = f ’ ( x ) cho bởi hình vẽ. Giá trị f ( 3 ) - 2 f ( 1 ) là
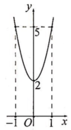
A. 30
B. 24
C. 26
D. 27
Biết hàm số
F
(
x
)
a
x
3
+
(
a
+
b
)
x
2
+
(
2
a
-
b
+
c
)
x
+
1
là một nguyên hàm của hàm số
f
(
x
)
3
x
2
+
6...
Đọc tiếp
Biết hàm số F ( x ) = a x 3 + ( a + b ) x 2 + ( 2 a - b + c ) x + 1 là một nguyên hàm của hàm số f ( x ) = 3 x 2 + 6 x + 2 . Tổng a+b+c là:
A. 5
B. 4
C. 3
D. 2
Cho hàm số
y
f
x
a
x
3
+
b
x
3
+
c
x
+
d
a
,
b
,
c
,
d
∈
ℝ
;
a
≠...
Đọc tiếp
Cho hàm số y = f x = a x 3 + b x 3 + c x + d a , b , c , d ∈ ℝ ; a ≠ 0 biết f'(-1)=3. Tính lim ∆ x → ∞ f 1 + ∆ x + f 1 ∆ x
A. 3
B. -3
C. 1
D. -1
Cho hàm số yf(x)x^3+ax^2+bx+4 có đồ thị (C) như hình vẽ. Hỏi (C) là đồ thị của hàm số yf(x) nào? A.
y
f
(
x
)
x
3
-
3
x
2
+
4
B.
y
f
(
x
)
x
3
+
6
x...
Đọc tiếp
Cho hàm số y=f(x)=x^3+ax^2+bx+4 có đồ thị (C) như hình vẽ. Hỏi (C) là đồ thị của hàm số y=f(x) nào?
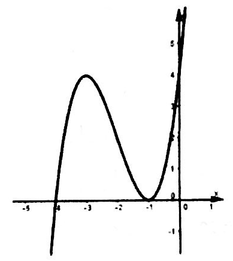
A. y = f ( x ) = x 3 - 3 x 2 + 4
B. y = f ( x ) = x 3 + 6 x 2 + 9 x + 4
C. y = f ( x ) = x 3 + 3 x 2 + 4
D. y = f ( x ) = x 3 - 6 x 2 + 9 x + 4
Cho hàm số
y
f
(
x
)
x
3
+
a
x
2
+
b
x
+
c
đạt cực tiểu bằng – 3 tại điểm x1 và đồ thị hàm số cắt trục tung tại điểm có tung độ là 2. Tính đạo hàm cấp một của hàm số tại x -3 A. f(-3) 0 B. f(-3) 2 C. f(-3) 1 D. f(-3) -2
Đọc tiếp
Cho hàm số y = f ( x ) = x 3 + a x 2 + b x + c đạt cực tiểu bằng – 3 tại điểm x=1 và đồ thị hàm số cắt trục tung tại điểm có tung độ là 2. Tính đạo hàm cấp một của hàm số tại x= -3
A. f'(-3)= 0
B. f'(-3)= 2
C. f'(-3)= 1
D. f'(-3)= -2
Biết hàm số
f
(
x
)
x
3
+
a
x
2
+
b
x
+
c
đạt cực tiểu tại điểm
x
1
,
f
(
1
)
-
3
và đồ thị của hàm số cắt trục tung tại điểm có tung độ bằng 2. Tính giá trị của hàm số tại
x
3
A. ...
Đọc tiếp
Biết hàm số f ( x ) = x 3 + a x 2 + b x + c đạt cực tiểu tại điểm x = 1 , f ( 1 ) = - 3 và đồ thị của hàm số cắt trục tung tại điểm có tung độ bằng 2. Tính giá trị của hàm số tại x = 3
A. f 3 = 81
B. f 3 = 27
C. f 3 = 29
D. f 3 = - 81
Cho các mệnh đề sau đây:(1) Hàm số
f
(
x
)
log
2
2
x
-
log
2
x
4
+
4
có tập xác định
D
[
0
;
+
∞
)
(2) Hàm số
y
log
a
x
có tiệm cận ngang(3) Hàm số
y
log
a
x
;
...
Đọc tiếp
Cho các mệnh đề sau đây:
(1) Hàm số f ( x ) = log 2 2 x - log 2 x 4 + 4 có tập xác định D = [ 0 ; + ∞ )
(2) Hàm số y = log a x có tiệm cận ngang
(3) Hàm số y = log a x ; 0 < a < 1 và Hàm số y = log a x , a > 1 đều đơn điệu trên tập xác định của nó
(4) Bất phương trình: log 1 2 5 - 2 x 2 - 1 ≤ 0 có 1 nghiệm nguyên thỏa mãn.
(5) Đạo hàm của hàm số y = ln 1 - cos x là sin x 1 - cos x 2
Hỏi có bao nhiêu mệnh đề đúng:
A. 0
B. 2
C. 3
D.1
Cho hàm số
f
(
x
)
ax
+
3
b
x
2
+
c
x
+
d
(
a
,
b
,
c
,
d
∈
R
)
có đồ thị như hình vẽ sau. Số nghiệm của phương trình 4f(x) + 3 0 là A. 3 B. 2 C. 1 D. 0
Đọc tiếp
Cho hàm số f ( x ) = ax + 3 b x 2 + c x + d ( a , b , c , d ∈ R ) có đồ thị như hình vẽ sau. Số nghiệm của phương trình 4f(x) + 3 = 0 là
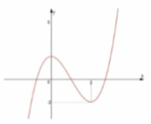
A. 3
B. 2
C. 1
D. 0
Cho hàm số yf(x) xác định trên R. Đồ thị hàm số
y
f
(
x
)
cắt trục hoành tại 3 điểm a, b, c (
a
b
c
) như hình dưới: Biết f(b) 0 Đồ thị hàm số yf(x) cắt trục hoành tại bao nhiêu điểm phân biệt. A. 4 B. 1 C. 0 D. 2
Đọc tiếp
Cho hàm số y=f(x) xác định trên R. Đồ thị hàm số y = f ' ( x ) cắt trục hoành tại 3 điểm a, b, c ( a < b < c ) như hình dưới:
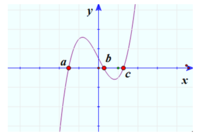
Biết f(b) < 0 Đồ thị hàm số y=f(x) cắt trục hoành tại bao nhiêu điểm phân biệt.
A. 4
B. 1
C. 0
D. 2

