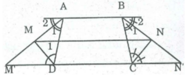
Gọi M' và N' là giao điểm của tia AM và BN với CD.
Ta có: ∠ (M') = ∠ A 2 (sole trong)
∠ A 1 = ∠ A 2 (gt)
⇒ ∠ (M') = ∠ A 1 nên ∆ ADM' cân tại D
* DM là phân giác của ∠ (ADM' )
Suy ra: DM là đường trung tuyến (tính chất tam giác cân)
⇒ AM = MM'
∠ (N') = ∠ B 1 nên ∆ BCN' cân tại C.
* CN là phân giác của ∠ (BCN')
Suy ra: CN là đường trung tuyến (tính chất tam giác cân)
⇒ BN = NN'
Suy ra: MN là đường trung bình của hình thang ABN'M'
⇒ MN // M'N' (tính chất đường trung hình hình thang)
Hay MN//CD

