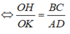Từ O kẻ đường thẳng song song với AB và CD cắt AD tại E, cắt BC tại F.
Áp dụng kết quả chứng minh ở bài 14 ta có:
OE = OF
Từ đó, ta có:
S A E O = S B F O (1) (hai tam giác có cùng đường cao và hai đáy bằng nhau);
S D E O = S C F O (2)
Từ (1) và (2) suy ra : S O A D = S O B C (3)
Suy ra: OH.AD = OK.BC
⇔